题目内容
8.如图,抛物线y=ax2+bx+c与x轴交于A(-1,0,)、B(3,0)两点与y轴交于点C(0,3),点D为抛物线的顶点.(1)求抛物线的解析式;
(2)设点P的坐标为(a,0),当|PD-PC|最大时,求a的值;
(3)在线段BC上方的抛物线上有一动点Q,当Q运动到何位置时,△BCQ的面积最大;
(4)在坐标平面内找一点E,使以B、C、D、E为顶点的四边形为平行四边形,直接写出E点坐标.
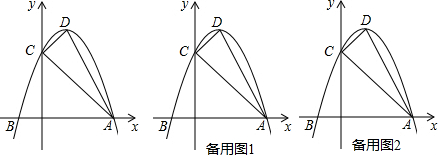
分析 (1)设交点式y=a(x+1)(x-3),然后把C点坐标代入求出a即可得到抛物线解析式;
(2)把解析式配成顶点式得到D点坐标,再利用待定系数法求出直线CD的解析式,于是可得到直线CD与x轴的交点坐标为(-3,0),利用三角形三边的关系得到|PD-PC|≤CD(当且仅当点P、C、D共线时,取等号),此时P点为直线CD与x轴的交点,从而得到a的值;
(3)作QK∥y轴交BC于Q,如图1,利用待定系数法求出直线BC的解析式为y=3x+3,设Q(x,-x2+2x+3),K(x,3x+3),则QK=-x2-x,所以S△BCQ=$\frac{1}{2}$•1•QK=-$\frac{1}{2}$x2-$\frac{1}{2}$x,然后根据二次函数的性质解决问题;
(4)讨论:当CD为对角线,利用平移可得到E点坐标为(2,7);当BD为对角线或BC为对角线时,利用同样方法求E点坐标.
解答 解:(1)设抛物线解析式为y=a(x+1)(x-3),
把C(0,3)代入得a•1•(-3)=3,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-3),即y=-x2+2x+3;
(2)y=-x2+2x+3=-(x-1)2+4,则D(1,4),
设直线CD的解析式为y=mx+n,
把C(0,3),D(1,4)代入得$\left\{\begin{array}{l}{n=3}\\{m+n=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$,
所以直线CD的解析式为y=x+3,
当y=0时,x+3=0,解得x=-3,则直线CD与x轴的交点坐标为(-3,0),
因为|PD-PC|≤CD(当且仅当点P、C、D共线时,取等号),此时P点为直线CD与x轴的交点,
所以a=-3;
(3)作QK∥y轴交BC于Q,如图1,
设直线BC的解析式为y=px+q,
把C(0,3),B(-1,0)代入得$\left\{\begin{array}{l}{q=3}\\{-p+q=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=3}\\{q=3}\end{array}\right.$,
所以直线BC的解析式为y=3x+3,
设Q(x,-x2+2x+3),K(x,3x+3),则QK=-x2+2x+3-(3x+3)=-x2-x,
S△BCQ=$\frac{1}{2}$•1•QK=-$\frac{1}{2}$x2-$\frac{1}{2}$x=-$\frac{1}{2}$(x+$\frac{1}{2}$)2+$\frac{1}{8}$,
当x=-$\frac{1}{2}$时,△BCQ的面积最大,此时Q点坐标为(-$\frac{1}{2}$,$\frac{7}{4}$);
(4)如图,当CD为对角线,E点坐标为(2,7);
当BD为对角线,E′点的坐标为(0,1);
当BC为对角线,E″点的坐标为(-2,-1).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会利用分类讨论的思想解决数学问题.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| A. | 20÷2.5=8 | B. | 8÷5=1.6 | C. | 1.2÷0.4=3 | D. | 42÷6=7 |
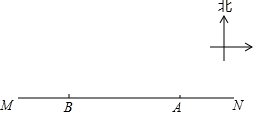 舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.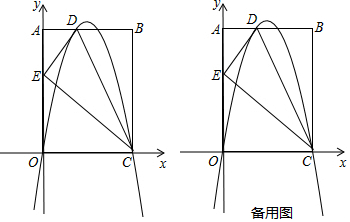
 如图,在平面直角坐标系中,顶点为(-4,1)的抛物线交y轴于A点,交x轴于B、C两点(点B在C的右侧),已知A点坐标为(0,-3).
如图,在平面直角坐标系中,顶点为(-4,1)的抛物线交y轴于A点,交x轴于B、C两点(点B在C的右侧),已知A点坐标为(0,-3).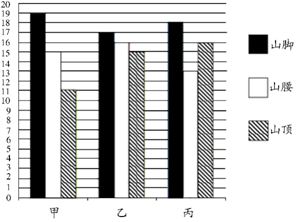 甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断: 在△ABC中,∠B的平分线交AC于D,∠C的平分线交AB于E,且BE=CD.
在△ABC中,∠B的平分线交AC于D,∠C的平分线交AB于E,且BE=CD.