题目内容
9. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路:

(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是24.
分析 (1)根据题意利用勾股定理表示出AD2的值,进而得出等式求出答案;
(2)根据题意利用勾股定理表示出FG2的值,进而得出等式求出答案.
解答 解:(1)如图,在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14-x,
由勾股定理得:AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
故152-x2=132-(14-x)2,
解得:x=9.
∴AD=12.
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×14×12=84.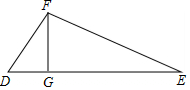 (2)如图,在△DEF中,DE=15,EF=13,DF=4,
(2)如图,在△DEF中,DE=15,EF=13,DF=4,
设GD=x,则GE=15-x,
由勾股定理得:FG2=DF2-GD2=42-x2,FG2=EF2-EG2=132-(15-x)2,
故42-x2=132-(15-x)2,
解得:x=2.4.
∴FG=3.2.
∴S△DEF=$\frac{1}{2}$DE•FG=$\frac{1}{2}$×15×3.2=24.
故答案为:24.
点评 此题主要考查了勾股定理,根据题意正确表示出AD2,FG2的值是解题关键.

练习册系列答案
相关题目
19.若(m-n)(m-n-2)-8=0,则m-n的值为( )
| A. | 4或-2 | B. | 4 | C. | -2 | D. | 2 |
17.某厂决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格,月处理污水量如表:
(1)经预算:治污部门购买污水处理设备的资金不超过105万元,你认为该部门有哪几种购买方案?
(2)在(1)的条件下,若每月要求处理的污水量不低于2040吨,为了节约资金,请你为该厂设计一种最省钱的购买方案.
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
(2)在(1)的条件下,若每月要求处理的污水量不低于2040吨,为了节约资金,请你为该厂设计一种最省钱的购买方案.
4.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2017次后形成的图形中所有正方形的面积和是( )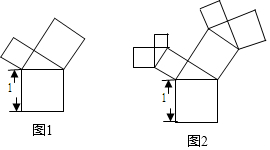

| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
14.已知x,y满足$\left\{\begin{array}{l}{2x-3y=1①}\\{3x-2y=5②}\end{array}\right.$,如果①×a+②×b可整体得到x+11y的值,那么a,b之间的关系式不正确的是( )
| A. | 2a+3b=1 | B. | 3a+2b=-11 | C. | a+b=2 | D. | a-b=-12 |
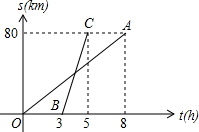 如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则: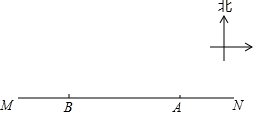 舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.