题目内容
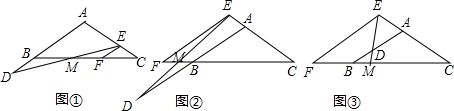
8.在等腰三角形ABC中,AB=AC,分别在射线AB、CA上取点D、E,连结DE,过点E作EF∥AB交直线BC于点F,直线BC与DE所在直线交于点M.猜想:如图①,点D在边AB延长线上,点E在边AC上,且BD=CE,则线段DM、EM的大小关系为DM=EM.
探究:如图②,点D、E分别在边AB、CA延长线上,且BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:如图③,点D在边AB上(点D不与点A、B重合),点E在边CA的延长线上,其它条件不变,若BD=1,CE=4,DM=0.7,则线段DE的长为2.1.
分析 (1)根据等腰三角形的性质和平行线的性质得到∠D=∠MEF,证明△BDM≌△FEM即可;
(2)根据等腰三角形的性质和平行线的性质得到∠D=∠MEF,证明△BDM≌△FEM即可;
(3)根据等腰三角形的性质和平行线的性质得到EF=CE由BD∥EF得$\frac{BD}{EF}$=$\frac{MD}{ME}$,代入数据即可得到结论.
解答 解:(1)猜想:DM=EM.
理由:∵AB=AC,
∴∠ABC=∠C,
∵EF∥AD,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
$\left\{\begin{array}{l}{∠D=∠FEM}\\{∠BMD=∠EMF}\\{BD=EF}\end{array}\right.$,
∴△BDM≌△FEM,
∴DM=EM.
故答案为:DM=EM.
(2)结论DM=EM.
理由:∵AB=AC,
∴∠ABC=∠C,
∵EF∥AB,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
$\left\{\begin{array}{l}{∠D=∠FEM}\\{∠BMD=∠EMF}\\{BD=EF}\end{array}\right.$,
∴△BDM≌△FEM,
∴DM=EM.
(3)∵EF∥AB,
∴∠F=∠ABC,
∵AB=AC,
∴∠ABC=∠C,
∴∠F=∠C,
∴EF=CE=4,
∵BD∥EF,
∴$\frac{BD}{EF}$=$\frac{MD}{ME}$,
∴$\frac{1}{4}$=$\frac{0.7}{EM}$,
∴EM=2.8,
∴DE=EM-DM=2.1,
故答案为2.1.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是添加辅助线构造全等三角形以及等腰三角形,属于中考常考题型.

| 老师在课堂上放手让学生提问和表达情况调查 | |||||
| 选项 | A | B | C | D | E |
| 内容 | 从不 | 很少 | 有时 | 常常 | 总是 |
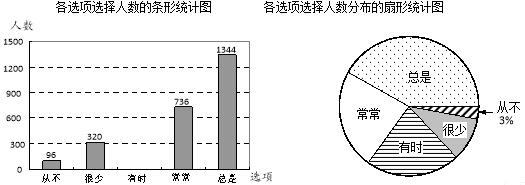
根据以上信息,解答下列问题:
(1)该区参加了本次问卷调查的八年级的学生共有多少名?
(2)请把这幅条形统计图补充完整.
(3)在扇形统计图中,“总是”所占的百分比多少?
 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )| A. | 22.5° | B. | 25° | C. | 23° | D. | 20° |
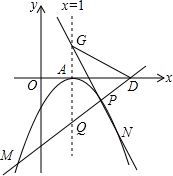 如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.
如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.