题目内容
14.旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入-管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
分析 (1)观光车全部租出每天的净收入=出租自行车的总收入-管理费,根据不等关系:净收入为正,列出不等式求解即可;
(2)由函数解析式是分段函数,在每一段内求出函数最大值,比较得出函数的最大值.
解答 解:(1)由题意知,若观光车能全部租出,则0<x≤100,
由50x-1100>0,
解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元;
(2)设每天的净收入为y元,
当0<x≤100时,y1=50x-1100,
∵y1随x的增大而增大,
∴当x=100时,y1的最大值为50×100-1100=3900;
当x>100时,
y2=(50-$\frac{x-100}{5}$)x-1100
=50x-$\frac{1}{5}$x2+20x-1100
=-$\frac{1}{5}$x2+70x-1100
=-$\frac{1}{5}$(x-175)2+5025,
当x=175时,y2的最大值为5025,
5025>3900,
故当每辆车的日租金为175元时,每天的净收入最多是5025元.
点评 本题用分段函数模型考查了一次函数,二次函数的性质与应用,解决问题的关键是弄清题意,分清收费方式.

练习册系列答案
相关题目
4.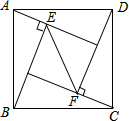 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )| A. | 7 | B. | 8 | C. | 7$\sqrt{2}$ | D. | 7$\sqrt{3}$ |
19. 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
6.化简$\frac{{m}^{2}}{m-n}$+$\frac{{n}^{2}}{n-m}$的结果是( )
| A. | m+n | B. | n-m | C. | m-n | D. | -m-n |
9.下列命题中,是真命题的为( )
| A. | 四个角相等的四边形是矩形 | |
| B. | 四边相等的四边形是正方形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是平行四边形 |