题目内容

11．如果一个正多边形的每个外角都是30°，那么这个多边形的内角和为1800°．

分析 根据正多边形的性质，边数等于360°除以每一个外角的度数，然后利用多边形的内角和公式计算内角和即可．

解答 解：∵一个多边形的每个外角都是30°，
∴n=360°÷30°=12，
则内角和为：（12-2）•180°=1800°．
故答案为：1800°．

点评 本题主要考查了利用外角求正多边形的边数的方法以及多边形的内角和公式，解题的关键是掌握任意多边形的外角和都等于360度．

练习册系列答案
相关题目
1．如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．
（1）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；
（2）当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．
①求证：BD⊥CF；
②当AB=2，AD=3$\sqrt{2}$时，求线段DH的长．
2．先化简，再求值：$（\frac{1}{x}-\frac{1}{x+2}）•\frac{{{x^2}-4}}{2}$，其中x=3．
19．如图，在平面直角坐标系中，点A的坐标为（4，3），那么cosα的值是（　　）
A．$\frac{3}{4}$B．$\frac{4}{3}$C．$\frac{3}{5}$D．$\frac{4}{5}$
6．化简$\frac{{m}^{2}}{m-n}$+$\frac{{n}^{2}}{n-m}$的结果是（　　）
A．m+nB．n-mC．m-nD．-m-n
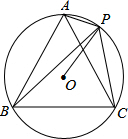1．如图，点P是等边三角形ABC外接圆⊙O上的点（点P与点A、B、C不重合），有下列结论：①当弦PB最长时，PA=PC；②当∠ACP=30°时，弦PB最长；③当PO⊥AB时，∠ACP=30°；④当△APC是等腰三角形时，PO⊥AC，其中正确结论的个数是（　　）
A．1B．2C．3D．4
8．在等腰三角形ABC中，AB=AC，分别在射线AB、CA上取点D、E，连结DE，过点E作EF∥AB交直线BC于点F，直线BC与DE所在直线交于点M．
猜想：如图①，点D在边AB延长线上，点E在边AC上，且BD=CE，则线段DM、EM的大小关系为DM=EM．
探究：如图②，点D、E分别在边AB、CA延长线上，且BD=CE，判断线段DM、EM的大小关系，并加以证明．
拓展：如图③，点D在边AB上（点D不与点A、B重合），点E在边CA的延长线上，其它条件不变，若BD=1，CE=4，DM=0.7，则线段DE的长为2.1．
5．计算：20+$\sqrt{8}$+|$\sqrt{2}$-2|=3+$\sqrt{2}$．
6．计算：|-5+3|的结果是（　　）
A．-8B．8C．-2D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网