题目内容
13．一个不透明的袋子，装了除颜色不同，其他没有任何区别的红色球3个，绿色球4个，黑色球7个，黄色球2个，从袋子中随机摸出一个球，摸到黑色球的概率是$\frac{7}{16}$．分析 先求出球的总数，再根据概率公式即可得出结论．
解答 解：∵红色球3个，绿色球4个，黑色球7个，黄色球2个，
∴球的总数=3+4+7+2=16，
∴摸到黑色球的概率=$\frac{7}{16}$．
故答案为：$\frac{7}{16}$．
点评 本题考查的是概率公式，熟知随机事件A的概率P（A）=事件A可能出现的结果数与所有可能出现的结果数的商是解答此题的关键．
练习册系列答案
相关题目
4．
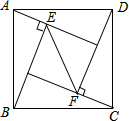如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB=∠CFD=90°，AE=CF=5，BE=DF=12，则EF的长是（ ）
如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB=∠CFD=90°，AE=CF=5，BE=DF=12，则EF的长是（ ）| A． | 7 | B． | 8 | C． | 7$\sqrt{2}$ | D． | 7$\sqrt{3}$ |
8．二次函数y=x2+2x-3的开口方向、顶点坐标分别是（ ）
| A． | 开口向上，顶点坐标为（-1，-4） | B． | 开口向下，顶点坐标为（1，4） | ||
| C． | 开口向上，顶点坐标为（1，4） | D． | 开口向下，顶点坐标为（-1，-4） |
18．
如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于（ ）
如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于（ ）| A． | 24° | B． | 34° | C． | 56° | D． | 124° |
