题目内容
5.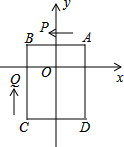 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )| A. | (-1,-1) | B. | (-1,1) | C. | (-2,2) | D. | (1,2) |
分析 利用行程问题中的相遇问题,由于矩形的边长为3和2,P、Q的速度和是5,求得每一次相遇的地点,找出规律即可解答.
解答 解:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2),
∴AB=CD=1-(-1)=2,BC=AD=1-(-2)=3,即AB+BC=5,
∴经过1秒钟时,P与Q在B(-1,1)处相遇,
接下来两个点走的路程为10的倍数时,两点相遇,
∵第二次相遇在CD的中点(0,-2),
第三次相遇在A(1,1),
第四次相遇在(-1,-1)
第五次相遇在(1,-1),
第六次相遇在B点(-1,1)
每五次相遇点重合一次,
2014÷5=402…4,
即第2014次相遇点的坐标与第四次相遇点的坐标重合,即(-1,-1).
故选:A.
点评 此题主要考查了行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
16.不论x取何值时,下列分式总有意义的是( )
| A. | $\frac{2+x}{x}$ | B. | $\frac{{x}^{2}+1}{2x}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{2x-1}{{x}^{2}+1}$ |
14.已知边长为a的正方形的面积为8,则下列说法中,错误的是( )
| A. | a是无理数 | B. | a是方程x2-8=0的解 | ||
| C. | a是8的算术平方根 | D. | a满足不等式$\frac{2x-4}{3}>1$ |
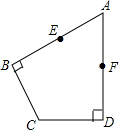 如图,在四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD=6,∠BAD=60°.
如图,在四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD=6,∠BAD=60°.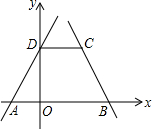 一次函数y=2x+2图象与x轴、y轴分别交于A、D两点,一次函数y=-2x+8与x轴交于B点,过D点作DC∥x轴,交直线y=-2x+8于点C.
一次函数y=2x+2图象与x轴、y轴分别交于A、D两点,一次函数y=-2x+8与x轴交于B点,过D点作DC∥x轴,交直线y=-2x+8于点C. 如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?
如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?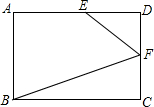 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.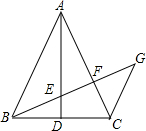 如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.
如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.