题目内容
9.在△ABC中,D、E分别在AB、AC上,AD=3,BD=2,AC=10,EC=4,则S△ADE:S△ABC=9:25.分析 根据已知条件得到$\frac{AD}{AB}$=$\frac{3}{5}$,$\frac{AE}{AC}=\frac{6}{10}=\frac{3}{5}$,于是得到$\frac{AD}{AB}=\frac{AE}{AC}$,推出△ADE∽△ABC,根据相似三角形的性质即可得到结论.
解答 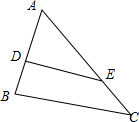 解:如图,
解:如图,
∵AD=3,BD=2,
∴AB=5,
∵$\frac{AD}{AB}$=$\frac{3}{5}$,$\frac{AE}{AC}=\frac{6}{10}=\frac{3}{5}$,
∴$\frac{AD}{AB}=\frac{AE}{AC}$,∵∠A=∠A,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=9:25,
故答案为:9:25.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个零件的形状如图所示,按规定∠A应等于120°,∠B、∠D应分别为15°、20°.李叔叔量得∠BCD=145°,就能断定该零件不合格,你能说出其中的道理吗?
一个零件的形状如图所示,按规定∠A应等于120°,∠B、∠D应分别为15°、20°.李叔叔量得∠BCD=145°,就能断定该零件不合格,你能说出其中的道理吗?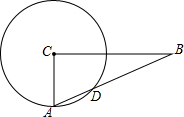 如图,在△ACB中,∠C=90°,∠B=20°,以C为圆心,AC长为半径的圆交AB于D点,若AC=6,求$\widehat{AD}$的长.
如图,在△ACB中,∠C=90°,∠B=20°,以C为圆心,AC长为半径的圆交AB于D点,若AC=6,求$\widehat{AD}$的长.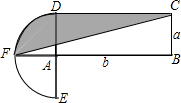 设计一个商标(如图阴影部分),其中A为半圆DFE的圆心,BC=a,AB=b,用关于a,b的代数式表示商标图案的面积S,并求a=4cm,b=8cm时S的值.
设计一个商标(如图阴影部分),其中A为半圆DFE的圆心,BC=a,AB=b,用关于a,b的代数式表示商标图案的面积S,并求a=4cm,b=8cm时S的值.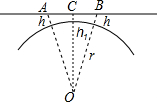 在著名的进化论辩论中,站在达尔文一边的学者瓦莱士曾经提出过一个非常简单而有趣的测量地球半径的方法:如图,在-条笔直的运河上树立两很木杆,其上端点A和点B之间的距离AB是可测量的,而且它们到水面的距离都是h,在两木杆的正中间树立第三根木杆,并且使其上端点C正好在AB连线上.由于地球的表面是一个曲面,所以运河的水面实际上也是弯曲的,故点C到水面的高度h1比h略小-点.由此可求出地球的半径.请问地球半径是多少呢?
在著名的进化论辩论中,站在达尔文一边的学者瓦莱士曾经提出过一个非常简单而有趣的测量地球半径的方法:如图,在-条笔直的运河上树立两很木杆,其上端点A和点B之间的距离AB是可测量的,而且它们到水面的距离都是h,在两木杆的正中间树立第三根木杆,并且使其上端点C正好在AB连线上.由于地球的表面是一个曲面,所以运河的水面实际上也是弯曲的,故点C到水面的高度h1比h略小-点.由此可求出地球的半径.请问地球半径是多少呢?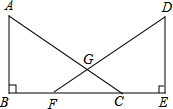 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证:
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证: