题目内容
15.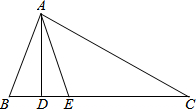 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,AD⊥BC,AE平分∠BAC.(1)若∠B=72°,∠C=30°,
求①∠BAE的度数;
②∠DAE的度数;
(2)探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
分析 (1)①先根据三角形内角和定理计算出∠BAC=78°,然后根据角平分线定义得到∠BAE=$\frac{1}{2}$∠BAC=39°;
②根据垂直定义得到∠ADB=90°,则利用互余可计算出∠BAD=90°-∠B=18°,然后利用∠DAE=∠BAE-∠BAD进行计算即可;
(2)由∠B+∠C+∠BAC=180°,∠B=∠C+42°可消去∠C得到∠BAC=222°-2∠B,则根据角平分线定义得到∠BAE=111°-∠B,接着在△ABD中利用互余得∠BAD=90°-∠B,然后利用∠DAE=∠BAE-∠BAD进行计算即可得到∠DAE=21°.
解答 解:(1)①∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-72°-30°=78°,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=39°;
②∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=18°,
∴∠DAE=∠BAE-∠BAD=39°-18°=21°;
(2)能.
∵∠B+∠C+∠BAC=180°,∠B=∠C+42°,
∴∠C=∠B-42°,
∴2∠B+∠BAC=222°,
∴∠BAC=222°-2∠B,
∵AE平分∠BAC,
∴∠BAE=111°-∠B,
在△ABD中,∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=(111°-∠B)-(90°-∠B)=21°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.掌握角平分线和高的定义,熟练进行角度的运算.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
5.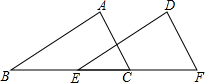 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )| A. | BC=EF | B. | ∠ACB=∠F | C. | ∠B=∠DEF | D. | AB=DE |
3.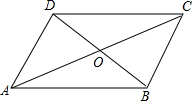 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )| A. | AB∥CD,AD∥BC | B. | AB∥CD,AD=BC | C. | AO=CO,BO=DO | D. | AB=CD,AD=BC |
10.下列各式中,能用平方差公式分解因式的是( )
| A. | a2+b2 | B. | -(a2+b2) | C. | -b2+a2 | D. | -a2-b2 |
4. 由于受台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树折断部分长度是( )
由于受台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树折断部分长度是( )
 由于受台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树折断部分长度是( )
由于受台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树折断部分长度是( )| A. | 8m | B. | 10m | C. | 16m | D. | 18m |
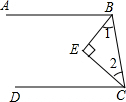 如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.
如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.