题目内容
6.计算(1)$\sqrt{5}+2\sqrt{5}-4\sqrt{5}$
(2)$\sqrt{81}+\root{3}{-27}+\sqrt{(-\frac{2}{3})^{2}}$
(3)$\sqrt{2}(\sqrt{2}-2)-(-1)^{2015}$
(4)|$\sqrt{3}$-2|-($\sqrt{5}$)2.
分析 (1)原式合并同类二次根式即可得到结果;
(2)原式利用平方根及立方根定义计算即可得到结果;
(3)原式利用二次根式的乘法法则及乘方的意义化简,计算即可得到结果;
(4)原式利用绝对值的代数意义及算术平方根定义计算即可得到结果.
解答 解:(1)原式=(1+2-4)$\sqrt{5}$=-$\sqrt{5}$;
(2)原式=9-3+$\frac{2}{3}$=6$\frac{2}{3}$;
(3)原式=2-2$\sqrt{2}$+1=3-2$\sqrt{2}$;
(4)原式=2-$\sqrt{2}$-5=-3-$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.计算(-$\frac{1}{2}$b2+2a)2等于( )
| A. | $\frac{1}{4}$b2-2ab2-4a2 | B. | $\frac{1}{4}$b4-2ab2+4a2 | C. | $\frac{1}{4}$b2ab2+4a2 | D. | -$\frac{1}{4}$b4+ab2-4a2 |
14.△ABC中,边AB=15,AC=13,高AD=12,则△ABC的周长是( )
| A. | 42 | B. | 32 | C. | 42或32 | D. | 不能确定 |
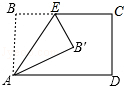 将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.
将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.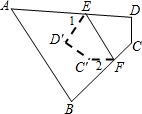 如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.
如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.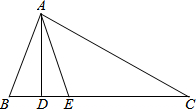 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,AD⊥BC,AE平分∠BAC.