题目内容
7.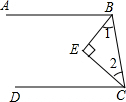 如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.
如图,已知BE、CE分别平分∠ABC、∠BCD,且∠1+∠2=90°,求证:AB∥CD.证明:如图,∵BE平分∠ABD(已知)
∴∠ABC=2∠1角平分线的定义
∵CE平分∠DCB(已知)
∴∠BCD=2∠2角平分线的定义
∴∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)
又∵∠1+∠2=90°(已知)
∴∠ABC+∠BCD=2×90°=180°,
∴AB∥CD同旁内角互补,两直线平行.
分析 先根据角平分线的定义得出∠ABC=2∠1,∠BCD=2∠2,再由∠1+∠2=90°可得出∠ABC+∠BCD=180°,由此可得出结论.
解答 证明:∵BE平分∠ABD(已知),
∴∠ABC=2∠1(角平分线的定义).
∵CE平分∠DCB(已知),
∴∠BCD=2∠2(角平分线的定义),
∴∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)
又∵∠1+∠2=90°(已知)
∴∠ABC+∠BCD=2×90°=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:∠ABC,角平分线的定义,∠BCD,角平分线的定义,∠ABC,∠BCD,同旁内角互补,两直线平行.
点评 本题考查的是平行线的判定,用到的知识点为:同旁内角互补,两直线平行.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
2.“4的平方根是±2”用数学式子表示为( )
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{4}$=±2 | C. | ±$\sqrt{4}$=2 | D. | $\sqrt{4}$=±2 |
17.以边长为1的正方形的一个顶点为坐标原点,经过这个顶点的两边为坐标轴建立平面直角坐标系,已知三个顶点的坐标分别为(0,0),(-1,0),(0,1),则第四个顶点的坐标为( )
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (1,-1) |
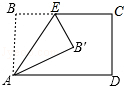 将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.
将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.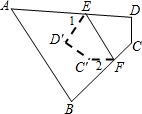 如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.
如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.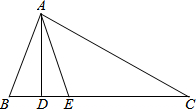 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,AD⊥BC,AE平分∠BAC.