Question

1．如图，MN表示一段笔直的高架道路，线段AB表示高架道路旁的一排居民楼，已知点A到MN的距离为15米，BA的延长线与MN相交于点D，且∠BDN=37°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．
（1）过点A作MN的垂线，垂足为点H，如果汽车沿着从M到N的方向在MN上行驶，当汽车到达点P处时，噪音开始影响这一排的居民楼，那么此时汽车与点H的距离为多少米？
（2）降低噪音的一种方法是在高架道路旁安装隔音板，当汽车行驶到点Q时，它与这一排居民楼的距离QC为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？（参考数据：sin37°=0.60，cos37°=0.80，tan37°=0.75）

Answer 1

分析 （1）连接PA．在直角△PAH中利用勾股定理来求PH的长度；
（2）由题意知，隔音板的长度是PQ的长度．通过解Rt△ADH、Rt△CDQ分别求得DH、DQ的长度，然后结合图形得到：PQ=PH+DQ-DH，把相关线段的长度代入求值即可．

解答 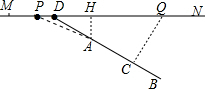解：（1）如图，连接PA．
由题意知，AP=39m．
在直角△APH中，PH=$\sqrt{A{{P}^{2}-AH}^{2}}$=$\sqrt{3{9}^{2}-1{5}^{2}}$=36（米），
答：此时汽车与点H的距离为36米；

（2）由题意知，隔音板的长度是PQ的长度．
在Rt△ADH中，DH=$\frac{AH}{tan37°}$=20（米）．
在Rt△CDQ中，DQ=$\frac{QC}{sin37°}$=65（米）．
则PQ=PH+HQ=PH+DQ-DH=36+65-20=81（米）．
答：高架道路旁安装的隔音板至少需要81米．

点评 本题考查了解直角三角形的应用、勾股定理的应用．根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案．