题目内容
11．
如图，正三角形ABC是⊙O的内接三角形，点P是劣弧AB上不同于点A、B的任意一点，则∠BPC的度数是（ ）| A． | 30° | B． | 45° | C． | 50° | D． | 60° |
分析 先根据等边三角形的性质求出∠BAC的度数，再由圆内接四边形的性质即可得出结论．
解答 解：∵△ABC是等边三角形，
∴∠BAC=60°．
∵∠BPC与∠BAC是同弧所对的圆周角，
∴∠BPC=∠BAC=60°．
故选D．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
2．
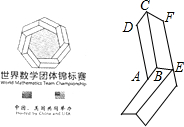第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行，其会徽如图所示，它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形．设AD=a，AB=b，CF=c，EF=d，则该会徽内外两个正七边形的周长之和为（ ）
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行，其会徽如图所示，它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形．设AD=a，AB=b，CF=c，EF=d，则该会徽内外两个正七边形的周长之和为（ ）| A． | 7（a+b+c-d） | B． | 7（a+b-c+d） | C． | 7（a-b+c+d） | D． | 7（b+c+d-a） |
19．
如图，直线a∥b∥c，直线m、n与a、b、c分别交于点A、C、E和B、D、F，若AC=4，AE=10，BF=$\frac{15}{2}$，则DF的长为（ ）
如图，直线a∥b∥c，直线m、n与a、b、c分别交于点A、C、E和B、D、F，若AC=4，AE=10，BF=$\frac{15}{2}$，则DF的长为（ ）| A． | $\frac{9}{2}$ | B． | 10 | C． | 3 | D． | $\frac{7}{2}$ |
6．关于x的方程（m-1）x2+2x+1=0有实数根，则m的取值范围是（ ）
| A． | m≤2 | B． | m＜2 | C． | m＜3且m≠2 | D． | m≤3且m≠2 |
3．下列各数中，比1大的数是（ ）
| A． | 0 | B． | -|-2| | C． | $\sqrt{2}$ | D． | -3 |
20．已知命题：等边三角形是等腰三角形．则下列说法正确的是（ ）
| A． | 该命题为假命题 | B． | 该命题为真命题 | ||
| C． | 该命题的逆命题为真命题 | D． | 该命题没有逆命题 |
如图，MN表示一段笔直的高架道路，线段AB表示高架道路旁的一排居民楼，已知点A到MN的距离为15米，BA的延长线与MN相交于点D，且∠BDN=37°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．