��Ŀ����
12��Сӱ�μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ������3��ѡ��ڶ�������4��ѡ���������Сӱ�����ᣬ����Сӱ����һ����������û��ʹ�ã�ʹ�á�����������������ȥ������һ���е�һ������ѡ�����1����Сӱ��һ���ⲻʹ�á�����������ôСӱ��Ե�һ����ĸ�����$\frac{1}{3}$��
��2����Сӱ�������������ڵڶ�����ʹ�ã���ôСӱ˳��ͨ�صĸ����Ƕ��٣�˵�����ɣ�
��3���Ӹ��ʵĽǶȷ�������Ὠ��Сӱ�ڴ�ڼ�����ʱʹ�á�����������ֱ�����𣬲���˵�����ɣ�
���� ��1��ֱ�����ø��ʹ�ʽ��⣻
��2������״ͼ����Z��ʾ��ȷѡ�C��ʾ����ѡ�չʾ����9�ֵȿ��ܵĽ�������ҳ�Сӱ˳��ͨ�صĽ������Ȼ����ݸ��ʹ�ʽ�����Сӱ˳��ͨ�صĸ��ʣ�
��3���루2������һ�����Сӱ�������������ڵ�һ����ʹ�ã�Сӱ˳��ͨ�صĸ��ʣ�Ȼ��Ƚ��������ʵĴ�С���ж�Сӱ�ڴ�ڼ�����ʱʹ�á���������
��� �⣺��1����Сӱ��һ���ⲻʹ�á�����������ôСӱ��Ե�һ����ĸ���=$\frac{1}{3}$��
�ʴ�Ϊ$\frac{1}{3}$��
��2����Сӱ�������������ڵڶ�����ʹ�ã���ôСӱ˳��ͨ�صĸ�����$\frac{1}{9}$���������£�
����״ͼΪ������Z��ʾ��ȷѡ�C��ʾ����ѡ�
����9�ֵȿ��ܵĽ����������Сӱ˳��ͨ�صĽ����Ϊ1��
����Сӱ˳��ͨ�صĸ���=$\frac{1}{9}$��
��2����Сӱ�������������ڵ�һ����ʹ�ã�����״ͼΪ������Z��ʾ��ȷѡ�C��ʾ����ѡ�
����8�ֵȿ��ܵĽ����������Сӱ˳��ͨ�صĽ����Ϊ1������Сӱ�������������ڵ�һ����ʹ�ã�Сӱ˳��ͨ�صĸ���=$\frac{1}{8}$��
����$\frac{1}{8}$��$\frac{1}{9}$��
���Խ���Сӱ�ڴ��һ����ʱʹ�á���������
���� ���⿼�����б�������״ͼ����ͨ���б�������״ͼ��չʾ���еȿ��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ����¼�A��B�ĸ��ʣ�

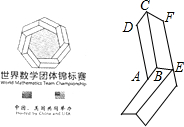 ������������ѧ�����������2015��11��25����11��29���ڱ������У�������ͼ��ʾ��������Χ����Χ�ֱ������߸����ı���ABCDȫ�ȵ��ı��κ��߸����ı���BEFCȫ�ȵ��ı������λ��ƶ��ɵ����߱��Σ���AD=a��AB=b��CF=c��EF=d����û�������������߱��ε��ܳ�֮��Ϊ��������
������������ѧ�����������2015��11��25����11��29���ڱ������У�������ͼ��ʾ��������Χ����Χ�ֱ������߸����ı���ABCDȫ�ȵ��ı��κ��߸����ı���BEFCȫ�ȵ��ı������λ��ƶ��ɵ����߱��Σ���AD=a��AB=b��CF=c��EF=d����û�������������߱��ε��ܳ�֮��Ϊ��������| A�� | 7��a+b+c-d�� | B�� | 7��a+b-c+d�� | C�� | 7��a-b+c+d�� | D�� | 7��b+c+d-a�� |
| A�� | 0 | B�� | -|-2| | C�� | $\sqrt{2}$ | D�� | -3 |
| A�� | ������������ | B�� | ������������ | ||
| C�� | �������������Ϊ������ | D�� | ������û�������� |
| A�� | a=$\sqrt{3}$��b=2��c=$\sqrt{7}$ | B�� | a=2��b=$\frac{2\sqrt{3}}{3}$��c=$\frac{4\sqrt{3}}{3}$ | C�� | a=$\frac{2\sqrt{3}}{3}$��b=2��c=$\frac{4\sqrt{3}}{3}$ | D�� | a=2��b=2��c=4 |
 ��ѧ��չ����������һСʱ���������ѧУʵ���������������A������ӣ�B������C��������D��ƹ���������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ���˶���Ŀ�������ȡ��һ����ѧ�����е��飬�������������Ƴ���������ͳ��ͼ��
��ѧ��չ����������һСʱ���������ѧУʵ���������������A������ӣ�B������C��������D��ƹ���������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ���˶���Ŀ�������ȡ��һ����ѧ�����е��飬�������������Ƴ���������ͳ��ͼ�� ��ͼ��MN��ʾһ�α�ֱ�ĸܵ�·���߶�AB��ʾ�ܵ�·�Ե�һ�ž���¥����֪��A��MN�ľ���Ϊ15�ף�BA���ӳ�����MN�ཻ�ڵ�D���ҡ�BDN=37�㣬���������ڸ��ٵ�·����ʻʱ����Χ39�����ڻ��ܵ�������Ӱ�죮
��ͼ��MN��ʾһ�α�ֱ�ĸܵ�·���߶�AB��ʾ�ܵ�·�Ե�һ�ž���¥����֪��A��MN�ľ���Ϊ15�ף�BA���ӳ�����MN�ཻ�ڵ�D���ҡ�BDN=37�㣬���������ڸ��ٵ�·����ʻʱ����Χ39�����ڻ��ܵ�������Ӱ�죮