题目内容
17.已知关于x的一元一次方程(m+3)x|m|-2+6m=0与$\frac{2x+1}{5}$-1=$\frac{x+n}{2}$的解相同,求代数式-2m2-mn的值.分析 根据一元一次方程解的定义得出m的值,代入求得一元一次方程(m+3)x|m|-2+6m=0的解,再把解代入$\frac{2x+1}{5}$-1=$\frac{x+n}{2}$即可得出n的值,再把m,n的值代入代数式-2m2-mn,求值即可.
解答 解:∵(m+3)x|m|-2+6m=0是关于x的一元一次方程,
∴|m|-2=1,且m+3≠0,得m=3;
可得一元一次方程为:6x+18=0,即x=-3;
把x=-3代入$\frac{2x+1}{5}$-1=$\frac{x+n}{2}$,得n=-1;
把m=3,n=-1代入-2m2-mn=-18+3=-15.
点评 本题考查了同解方程,掌握一元一次方程的定义和同解方程的定义是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
12.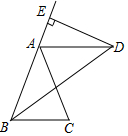 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
2.若a>b,则下列不等式中成立的是( )
| A. | a-5>b-5 | B. | $\frac{a}{5}$<$\frac{b}{5}$ | C. | a+5>b+6 | D. | -a>-b |
9.下面计算正确的是( )
| A. | (-3)2=-9 | B. | (-2)3=-8 | C. | $\sqrt{16}$=±4 | D. | -$\root{3}{-8}$=-2 |
 小强骑自行车去郊游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小强9点离开家,15点回家,根据这个图象,请你回答下列问题:
小强骑自行车去郊游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小强9点离开家,15点回家,根据这个图象,请你回答下列问题: