题目内容
12.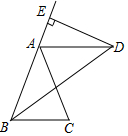 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
分析 (1)由BD平分∠ABC,得到∠ABD=∠DBC 根据等腰三角形的性质得到∠D=∠ABD等量代换得到∠D=∠DBC,于是得到结论;
(2)解①作DF⊥BC于F.根据角平分线的性质即可得到结论;②根据角平分线的定义得到∠ABC=2∠ABD=70°,由平行线的性质得到∠ACB=∠DAC=70°,于是得到结论.
解答 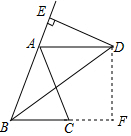 (1)证明:∵BD平分∠ABC,
(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBC
又∵AB=AD
∴∠D=∠ABD
∴∠D=∠DBC,
∴AD∥BC;
(2)解:①作DF⊥BC于F.
∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DF=DE=6(cm),
②∵BD平分∠ABC,
∴∠ABC=2∠ABD=70°,
∵AD∥BC,
∴∠ACB=∠DAC=70°,
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-70°=40°.
点评 本题考查了等腰三角形的性质,平行线的判定,角平分线的定义,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
7.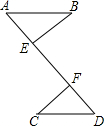 如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
 如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )| A. | AB=DC,∠B=∠C | B. | AB=DC,AB∥CD | C. | AB=DC,BE=CF | D. | AB=DF,BE=CF |
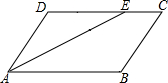 如图,在?ABCD中,∠BAD的平分线AE交边CD于点E,AB=5cm,BC=3cm,则EC=2cm.
如图,在?ABCD中,∠BAD的平分线AE交边CD于点E,AB=5cm,BC=3cm,则EC=2cm.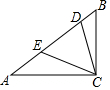 如图,在Rt△ABC的斜边AB上取两点D,E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数.
如图,在Rt△ABC的斜边AB上取两点D,E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数. 如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G,
如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G,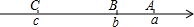 如图,已知数轴上A,B,C三点对应的数分别为a,b,c,化简|a-b|+|c-b|+|c-a|=2a-2c.
如图,已知数轴上A,B,C三点对应的数分别为a,b,c,化简|a-b|+|c-b|+|c-a|=2a-2c.