题目内容
5.为提升青少年的身体素质,深圳市在全市中小学推行“阳光体育”活动,某学校为满足学生的需求,准备再购买一些篮球和足球,已知用800元购买篮球的个数比购买足球的个数少2个,足球的单价为篮球单价的$\frac{4}{5}$.(1)求篮球、足球的单价分别为多少元?
(2)如果计划用不多于5200元购买篮球、足球共60个,那么至少要购买多少个足球?
分析 (1)设篮球的单价为x元/个,则足球的单价为0.8x元/个,根据用800元购买篮球的个数比购买足球的个数少2个,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)购买m个足球,则购买(60-m)个篮球,根据总价=单价×购买数量结合总价钱不多于5200元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,取其内的最小正整数即可.
解答 解:(1)设篮球的单价为x元/个,则足球的单价为0.8x元/个,
根据题意得:$\frac{800}{x}$+2=$\frac{800}{0.8x}$,
解得:x=100,
经检验,x=100是原方程的解,
∴0.8x=80.
答:篮球的单价为100元/个,足球的单价为80元/个.
(2)设购买m个足球,则购买(60-m)个篮球,
根据题意得:80m+100(60-m)≤5200,
解得:m≥40.
答:至少要购买40个足球.
点评 本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,列出分式方程;(2)根据总价=单价×购买数量结合总价钱不多于5200元,列出关于m的一元一次不等式.

练习册系列答案
相关题目
20.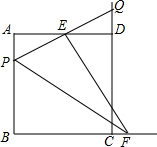 在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )
在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )
 在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )
在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )| A. | ①② | B. | ①②④ | C. | ②③④ | D. | ①②③ |
17.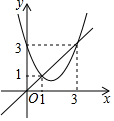 函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
 函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )| A. | 当1<x<3时,x2+(b-1)x+c<0 | B. | b+c=1 | ||
| C. | 3b+c=6 | D. | b2-4c>0 |
15.已知a<b,下列不等式中,变形正确的是( )
| A. | a-3>b-3 | B. | 3a-1>3b-1 | C. | -3a>-3b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
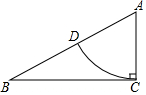 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于$\frac{π}{3}$.(结果保留π)
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于$\frac{π}{3}$.(结果保留π)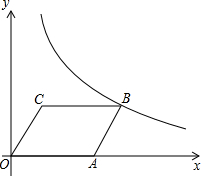 如图,?ABCO放置在平面直角坐标系中,已知A(6,0),C(3,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.
如图,?ABCO放置在平面直角坐标系中,已知A(6,0),C(3,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B. 如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为105°.
如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为105°.