题目内容
15．若点A（-1，a）在反比例函数y=-$\frac{3}{x}$的图象上，则a的值为3．分析 根据点A的横坐标，利用反比例函数图象上点的坐标特征，即可求出a值．
解答 解：∵点A（-1，a）在反比例函数y=-$\frac{3}{x}$的图象上，
∴a=-$\frac{3}{-1}$=3．
故答案为：3．
点评 本题考查了反比例函数图象上点的坐标特征，将点A的横坐标代入反比例函数解析式中求出a值是解题的关键．
练习册系列答案
相关题目
18．下列运算正确的是（ ）
| A． | 2a5-3a5=a5 | B． | a2•a3=a6 | C． | a7÷a5=a2 | D． | （a2b）3=a5b3 |
如图，直线y=-2x-4与坐标轴交于A、B两点，点P为直线y=2x上一点，且△ABP的面积被y轴分成1：2的两部分，求点P的坐标．
已知一次函数y=kx+b的图象经过点A（1，3）和B（-1，-1）两点．
直线y=kx+b（k≠0）的图象如图所示，由图象可知当y＜0时，x的取值范围是x＜2．
7．
如图，在△ABC中，AD平分∠BAC，按如下步骤作图：
步骤1：分别以点A，D为圆心，以大于$\frac{1}{2}$AD的长为半径，在AD两侧作弧，两弧交于点M，N；
步骤2：连接MN，分别交AB，AC于点E，F；
步骤3：连接DE，DF．
下列叙述不一定成立的是（ ）
如图，在△ABC中，AD平分∠BAC，按如下步骤作图：步骤1：分别以点A，D为圆心，以大于$\frac{1}{2}$AD的长为半径，在AD两侧作弧，两弧交于点M，N；
步骤2：连接MN，分别交AB，AC于点E，F；
步骤3：连接DE，DF．
下列叙述不一定成立的是（ ）
| A． | 线段DE是△ABC的中位线 | B． | 四边形AFDE是菱形 | ||
| C． | MN垂直平分线段AD | D． | $\frac{BD}{DC}$=$\frac{BE}{EA}$ |
4．
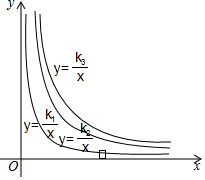甲、乙、丙三人直立在相同大小的平板上，平板对水平地面的压强y（帕）与平板面积x（m）的关系分别如图中的y=$\frac{{k}_{1}}{x}$，y=$\frac{{k}_{2}}{x}$，y=$\frac{{k}_{3}}{x}$，则当平板面积增加量相同时，甲、乙、丙三人所站的平板对水平地面的压强变化的关系是（ ）
甲、乙、丙三人直立在相同大小的平板上，平板对水平地面的压强y（帕）与平板面积x（m）的关系分别如图中的y=$\frac{{k}_{1}}{x}$，y=$\frac{{k}_{2}}{x}$，y=$\frac{{k}_{3}}{x}$，则当平板面积增加量相同时，甲、乙、丙三人所站的平板对水平地面的压强变化的关系是（ ）| A． | 甲的压强增加量＞乙压强增加量＞乙压强增加量 | |
| B． | 甲的压强减少量＞乙压强减少量＞乙压强减少量 | |
| C． | 乙的压强减少量＞甲压强减少量＞丙的压强减少量 | |
| D． | 丙的压强减少量＞乙压强减少量＞甲压强减少量 |