题目内容
20.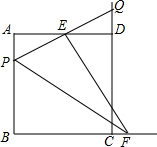 在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )
在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )| A. | ①② | B. | ①②④ | C. | ②③④ | D. | ①②③ |
分析 利用正方形的性质、全等三角形的性质、勾股定理等知识一一判断即可;
解答 解:①∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠B=90°,
∵∠A=∠EDQ,∠AEP=∠QED,AE=ED,
∴△AEP≌△DEQ,故①正确,
②作PG⊥CD于G,EM⊥BC于M,
∴∠PGQ=∠EMF=90°,
∵EF⊥PQ,
∴∠PEF=90°,
∴∠PEN+∠NEF=90°,∵∠NPE+∠NEP=90°,
∴∠NPE=∠NEF,
∵PG=EM,
∴△EFM≌△PQG,
∴EF=PQ,故②正确,
③连接QF.则QF=PF,PB2+BF2=QC2+CF2,设CF=x,
则(2+x)2+12=32+x2,
∴x=1,故③错误,
④当P在A点时,Q与D重合,QC的中点H在DC的中点S处,当P运动到B时,QC的中点H与D重合,
故EH扫过的面积为△ESD的面积的一半为$\frac{1}{2}$,故④正确.
故选B.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题.

练习册系列答案
相关题目
11.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2017个图形中直角三角形的个数有( )
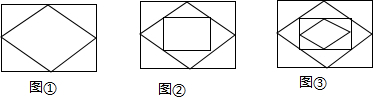

| A. | 8072个 | B. | 4036个 | C. | 4032个 | D. | 2016个 |
15.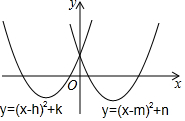 图中是有相同最小值的两条抛物线,则下列关系中正确的是( )
图中是有相同最小值的两条抛物线,则下列关系中正确的是( )
 图中是有相同最小值的两条抛物线,则下列关系中正确的是( )
图中是有相同最小值的两条抛物线,则下列关系中正确的是( )| A. | k<n | B. | h=m | C. | k+n=0 | D. | h<0,m>0 |
12.在同一直角坐标系中,若直线y=k1x与双曲线y=$\frac{{k}_{2}}{x}$没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
9.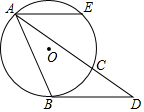 如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
 如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )| A. | 25° | B. | 50° | C. | 65° | D. | 70° |
 直线y=kx+b(k≠0)的图象如图所示,由图象可知当y<0时,x的取值范围是x<2.
直线y=kx+b(k≠0)的图象如图所示,由图象可知当y<0时,x的取值范围是x<2.