题目内容
10.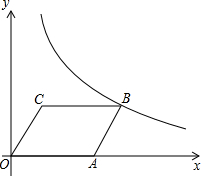 如图,?ABCO放置在平面直角坐标系中,已知A(6,0),C(3,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.
如图,?ABCO放置在平面直角坐标系中,已知A(6,0),C(3,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.(1)求此反比例函数的表达式;
(2)若点M(a,b)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且满足∠MCB>∠ABC,则a的取值范围是0<a<3$\sqrt{3}$.
分析 (1)根据平行四边形的性质及A点和C的坐标求出点B的坐标,然后根据待定系数法即可求得反比例函数得解析式;
(2)延长OC交反比例函数图象于点D,利用待定系数法求出直线BOC的解析式,联立直线与反比例函数解析式成方程组求出交点D的横坐标即可得出结论.
解答 解:(1)∵四边形ABCO是平行四边形,O为坐标原点,点A的坐标是(6,0),点C的坐标是(3,4),
∴BC=OA=6,6+3=9,
∴点B的坐标是(9,4),
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,
∴k=9×4=36,
∴反比例函数的表达式为y=$\frac{36}{x}$;
(2)延长OC交反比例函数图象于点D,如图所示.
∵四边形ABCO是平行四边形,
∴AB∥OC,
∴∠BCD=ABC,
∵点C(3,4),
∴直线OC的解析式为y=$\frac{4}{3}$x.
联立OC与反比例函数解析式得:$\left\{\begin{array}{l}{y=\frac{4}{3}x}\\{y=\frac{36}{x}}\end{array}\right.$,
解得:x1=3$\sqrt{3}$,x2=-3$\sqrt{3}$,
∵x>0,
∴点D的横坐标为3$\sqrt{3}$,
∴a<3$\sqrt{3}$,
故答案为0<a<3$\sqrt{3}$.
点评 本题考查了待定系数法求反比例函数和一次函数得解析式,反比例函数图象上点的坐标特征,平行四边形的性质、坐标与图形性质;熟练掌握平行四边形的性质和反比例函数图象上点的坐标特征是解决问题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
18.下列命题中,正确的是( )
| A. | 对角线相等的平行四边形是菱形 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 同位角相等 | |
| D. | 直角三角形斜边上的中线等于斜边的一半 |
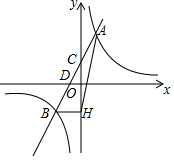 一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH. 如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为(6053,2).
如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为(6053,2).