题目内容
13.已知,一次函数y=kx+b的图象经过点(3,-3),且与直线y=4x-3的交点在x轴上.(1)求这个一次函数的解析式;
(2)求一次函数y=kx+b图象与坐标轴围成的三角形的面积.
分析 (1)根据一次函数y=kx+b的图象与直线y=4x-3的交点在x轴上,把y=0代入直线y=4x-3中求出x的值,确定出交点坐标,将两点坐标代入求出k与b的值,即可确定出直线的解析式;
(2)根据直线的解析式先求得直线与y轴的交点坐标,然后根据三角形的面积公式即可求解.
解答 解:(1)∵一次函数y=kx+b的图象与直线y=4x-3的交点在x轴上,
∴将y=0代入y=4x-3得:x=$\frac{3}{4}$,即($\frac{3}{4}$,0),
把(3,-3),($\frac{3}{4}$,0)代入得:
$\left\{\begin{array}{l}{3k+b=-3}\\{\frac{3}{4}k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=1}\end{array}\right.$,
∴直线解析式为y=-$\frac{4}{3}$x+1.
(2)∵直线解析式为y=-$\frac{4}{3}$x+1,
∴直线与y轴的交点为C(0,1),
而直线与x轴的交点为B($\frac{3}{4}$,0),
∴OB=$\frac{3}{4}$,OC=1,
∴S△OBC=$\frac{1}{2}$OB•OC=$\frac{1}{2}$×$\frac{3}{4}$×1=$\frac{3}{8}$,
即直线y=kx+b与坐标轴围成的三角形的面积为$\frac{3}{8}$.
点评 本题考查了用待定系数法求函数解析式,坐标轴上点的坐标特点以及三角形的面积公式的运用.求一次函数y=kx+b,则需要两组x,y的值.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
4.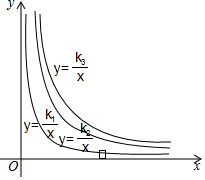 甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )
甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )
 甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )
甲、乙、丙三人直立在相同大小的平板上,平板对水平地面的压强y(帕)与平板面积x(m)的关系分别如图中的y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,则当平板面积增加量相同时,甲、乙、丙三人所站的平板对水平地面的压强变化的关系是( )| A. | 甲的压强增加量>乙压强增加量>乙压强增加量 | |
| B. | 甲的压强减少量>乙压强减少量>乙压强减少量 | |
| C. | 乙的压强减少量>甲压强减少量>丙的压强减少量 | |
| D. | 丙的压强减少量>乙压强减少量>甲压强减少量 |
18.下列命题中,正确的是( )
| A. | 对角线相等的平行四边形是菱形 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 同位角相等 | |
| D. | 直角三角形斜边上的中线等于斜边的一半 |
 已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1)两点.
已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1)两点.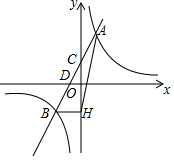 一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.