题目内容
4.m是方程x2+x-1=0的根,则m3+2m2+2009的值为( )| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
分析 把m代入x2+x-1=0得到m2+m-1=0,即m2+m=1,把m2+m=1代入式子:m3+2m2+2009,再将式子变形为m(m2+m)+m2+2009的形式,即可求出式子的值.
解答 解:∵m是方程x2+x-1=0的根,
∴m2+m-1=0,即m2+m=1,
∴m3+2m2+2009=m(m2+m)+m2+2009=m+m2+2009=1+2009=2010.
故选B.
点评 本题考查了一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了代数式求值,本题代数式中的字母表示的数没有明确告知,而是隐含在题设中,首先应从题设中获取代数式m2+m的值,然后利用“整体代入法”求代数式的值.

练习册系列答案
相关题目
13.把点A(2,-3)平移后得到点B(-2,3),则平移的过程是( )
| A. | 先向左平移4个单位长度,在向下平移6个单位长度 | |
| B. | 先向左平移4个单位长度,再向上平移6个单位长度 | |
| C. | 先向右平移4个单位长度,在向下平移6个单位长度 | |
| D. | 先向右平移4个单位长度,在向上平移6个单位长度 |
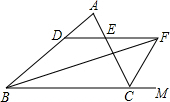 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E.问:
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E.问: