题目内容
12.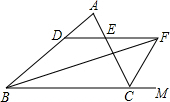 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E.问:
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E.问:(1)找出图中所有的等腰三角形,并加以证明;
(2)线段BD、CE、DE之间存在着怎样的数量关系?为什么?
分析 (1)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(2)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE.
解答  (1)解:图中有2个等腰三角形即△BDF和△CEF,
(1)解:图中有2个等腰三角形即△BDF和△CEF,
∵BF、CF分别平分∠ABC、∠ACB的外角,
∴∠DBF=∠CBF,∠FCE=∠FCM,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCM,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴△BDF和△CEF为等腰三角形;
(2)存在:BD-CE=DE,
证明:∵DF=BD,CE=EF,
∴BD-CE=FD-EF=DE.
点评 本题主要考查了等腰三角形的性质,利用边角关系并结合等量代换来推导证明.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
4.m是方程x2+x-1=0的根,则m3+2m2+2009的值为( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
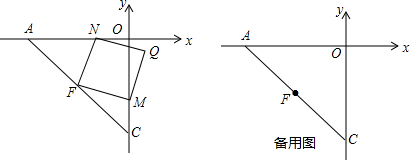
 如图,∠B=∠C=90°,BC=10,AM平分∠DAB,DM平分∠ADC,则点M到AD的距离为5.
如图,∠B=∠C=90°,BC=10,AM平分∠DAB,DM平分∠ADC,则点M到AD的距离为5.