题目内容
19.已知正比例函数y=kx(k是常数,k≠0),当-3≤x≤1时,对应的y的取值范围是-1≤y≤$\frac{1}{3}$,且y随x的减小而减小,则k的值为$\frac{1}{3}$.分析 由一次函数的性质,进行运算求解.
解答 解:易知k>0时,y随x的减少而减少,
∴当x=-3时,y=-1,代入正比例函数y=kx得:-1=-3k
解得k=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 此题考查一次函数的性质,要注意根据一次函数图象的性质来分析.

练习册系列答案
相关题目
14.如果$\frac{1}{{s}_{1}}=\frac{1}{{t}_{1}}+\frac{1}{{t}_{2}}$,$\frac{1}{{s}_{2}}=\frac{1}{{t}_{1}}-\frac{1}{{t}_{2}}$,则$\frac{{s}_{1}}{{s}_{2}}$=( )
| A. | $\frac{{t}_{1}+{t}_{2}}{{t}_{2}-{t}_{1}}$ | B. | $\frac{{t}_{2}-{t}_{1}}{{t}_{2}+{t}_{1}}$ | C. | $\frac{{t}_{1}-{t}_{2}}{{t}_{2}+{t}_{1}}$ | D. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ |
4.m是方程x2+x-1=0的根,则m3+2m2+2009的值为( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
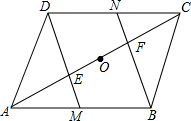 已知如图,O是?ABCD对角线AC的中点,E是AO的中点,F是OC的中点,联结DE并延长交AB于点M,联结BF并延长交CD于点N,求证:四边形DMBN是平行四边形.
已知如图,O是?ABCD对角线AC的中点,E是AO的中点,F是OC的中点,联结DE并延长交AB于点M,联结BF并延长交CD于点N,求证:四边形DMBN是平行四边形. 如图,点D是等腰△ABC底边BC上任意一点,DE∥AC交AB于点E,DF∥AB交AC于点F,求证:DE+DF=AB.
如图,点D是等腰△ABC底边BC上任意一点,DE∥AC交AB于点E,DF∥AB交AC于点F,求证:DE+DF=AB. 如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,以格点为顶点按照要求作图:
如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,以格点为顶点按照要求作图: