题目内容
当x满足什么条件时,下列不等关系成立?
(1)2(1-3x)>3x+20;
(2)
(x-1)≤
(4x-5).
(1)2(1-3x)>3x+20;
(2)
| 1 |
| 2 |
| 1 |
| 3 |
考点:解一元一次不等式
专题:
分析:(1)先去括号,再移项,合并同类项,系数化为1即可.
(2)先去分母、去括号,再移项,合并同类项,系数化为1即可.
(2)先去分母、去括号,再移项,合并同类项,系数化为1即可.
解答:解:(1)去括号,得2-6x>3x+20,
移项,合并同类项,得-9x>-18,
系数化为1,得x<2;
(2)去分母,得3(x-1)≤2(4x-5),
去括号,得3x-3≤8x-10,
再移项,合并同类项,得-5x≤-7,
系数化为1,得x≥
.
移项,合并同类项,得-9x>-18,
系数化为1,得x<2;
(2)去分母,得3(x-1)≤2(4x-5),
去括号,得3x-3≤8x-10,
再移项,合并同类项,得-5x≤-7,
系数化为1,得x≥
| 7 |
| 5 |
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
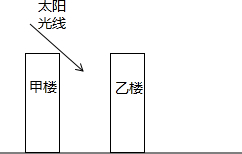 甲楼楼高50米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°,此时,求:
甲楼楼高50米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°,此时,求: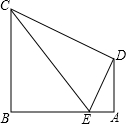 如图,四边形ABCD中,AD⊥AB,BC⊥AB,BC=2AD,DE⊥CD交边AB于E,连接CE,若△CDE与四边形ABCD的面积之比为2:5,则cos∠BCE的值为
如图,四边形ABCD中,AD⊥AB,BC⊥AB,BC=2AD,DE⊥CD交边AB于E,连接CE,若△CDE与四边形ABCD的面积之比为2:5,则cos∠BCE的值为 如图,CD平分∠ACB,DE∥AC,若∠1=76°,则∠EDC=
如图,CD平分∠ACB,DE∥AC,若∠1=76°,则∠EDC=