Question

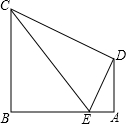如图，四边形ABCD中，AD⊥AB，BC⊥AB，BC=2AD，DE⊥CD交边AB于E，连接CE，若△CDE与四边形ABCD的面积之比为2：5，则cos∠BCE的值为

 

．

Answer 1

考点：勾股定理,整式的混合运算,三角形的面积

专题：

分析：∠CDE=∠A，∠DEA=∠CED对应相等，从而证明△DEC∽△AED．设S_△CDE=2S，S_梯形ABCD=5S，得出AD=

DE2-AE2

=

5

AE，BE=

CE2-BC2

=4AE，即可得出sin∠BCE=BE：CE的比值，进一步得到cos∠BCE的值即为所求．

解答：解：过点D作DF⊥BC于F，DF交CE于G，则ADFB是矩形．
∴BF=AD，
∴CF=BC-BF=2AD-AD=AD=BF，即F是BC的中点，
∵FG∥BE，
∴FG是△CBE的中位线，
∴CG=GE，
∵∠CDE=90°，
∴DG是直角△CDE斜边上的中线，
∴DG=GE，
∴∠GDE=∠GED．
∵GD∥AB，
∴∠GDE=∠DEA．
∴∠GED=∠DEA．
又∵∠CDE=∠A=90°，
∴△DEC∽△AED．
∴DE：AE=CE：DE．
∴DE²=AE•CE．
延长BA，CD交于点G．
设S_△CDE=2S，S_梯形ABCD=5S，
∵S_△DEG=2S，
又∵S_△ADG：S_△GBC=AD²：BC²=1：4，
∴S_△ADG：（S_△ADG+5S）=1：4，
∴S_△ADG=

5

3

S，
∴S_△ADE=2S-

5

3

S=

1

3

S，
∴（

AE

DE

）²=

S△ADE

S△CDE

=

1

6

，
∴DE=

6

AE，
∵CE=

DE2

AE

=6AE，
又∵AD=

DE2-AE2

=

5

AE，
∴BC=2

5

AE，
∴BE=

CE2-BC2

=4AE，
∴sin∠BCE=BE：CE=

2

3

，
∴cos∠BCE=

5

3

．
故答案为：

5

3

．

点评：考查了相似三角形的判定和性质，以及求三角函数值．同时涉及三角形的面积，本题较难．