题目内容
因式分解：
（1）x（x-y）（a-b）-y（y-x）（b-a）
（2）2x3y+8x2y2+8xy3．
（1）x（x-y）（a-b）-y（y-x）（b-a）
（2）2x3y+8x2y2+8xy3．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）首先把式子变形为x（x-y）（a-b）-y（x-y）（a-b），再提取公因式x-y即可；
（2）首先提取公因式2xy，再利用完全平方公式进行二次分解即可．
（2）首先提取公因式2xy，再利用完全平方公式进行二次分解即可．
解答：解：（1）原式=x（x-y）（a-b）-y（x-y）（a-b）=（x-y）（x-y）（a-b）=（x-y）2（a-b）；
（2）原式=2xy（x2+4xy+4y2）=2xy（x+2y）2．
（2）原式=2xy（x2+4xy+4y2）=2xy（x+2y）2．
点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
练习册系列答案
应用题作业本系列答案
相关题目
如图，AD是等腰△ABC的底边BC上的中线，P是直线AD上任意一点，求证：BP=CP．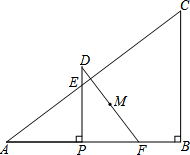
如图，在Rt△ABC中，∠B=90°，AB=20cm，BC=15cm，动点P从点A出发，以每秒4cm的速度沿AB方向运动，到达点B时停止运动．过点P作AB的垂线交斜边AC于点E，将△APE绕点P顺时针旋转90°得到△DPF．设点P在边AB上运动的时间为t（秒）．
已知一次函数y=kx+b的图象是过A（0，-4），B（2，-3）两点的一条直线．