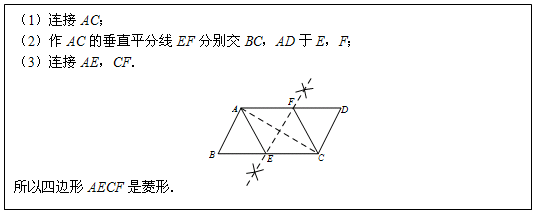
题目内容
8．求2a2-4a-4ab+5b2-8b+2031的最小值．分析 多项式配方变形后，利用非负数的性质求出多项式的最小值，．
解答 解：2a2-4a-4ab+5b2-8b+2031=（a2-4a+4）+（a2-4ab+4b2）+（b2-8b+16）+2011=（a-2）2+（a-2b）2+（b-4）2+2011．
∵（a-2）2+（a-2b）2+（b-4）2+2011≥2011，
∴2a2-4a-4ab+5b2-8b+2031的最小值是2011，
点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
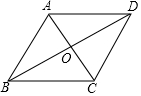如图，若使菱形ABCD是正方形，则需添加的条件是∠ABC=90°或∠DAB=90°或∠ADC=90°或∠BCD=90°或AC=BD．（填上一个符合题目要求的条件即可）
一个正三棱柱的三视图如图所示，若这个正三棱柱的表面积为24+8$\sqrt{3}$，则a的值是2．
