题目内容
17.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3、…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( $\frac{\sqrt{3}}{3}$)2015.
分析 利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.
解答 解:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=$\frac{1}{2}$,
则B2C2=$\frac{{B}_{2}{E}_{2}}{cos30°}$=($\frac{\sqrt{3}}{3}$)1,
同理可得:B3C3=$\frac{1}{3}$=( $\frac{\sqrt{3}}{3}$)2,
故正方形AnBnCnDn的边长是:( $\frac{\sqrt{3}}{3}$)n-1,
则正方形A2016B2016C2016D2016的边长为:( $\frac{\sqrt{3}}{3}$)2015,
故答案为:( $\frac{\sqrt{3}}{3}$)2015.
点评 此题主要考查了正方形的性质以及锐角三角函数关系,得出正方形的边长变化规律是解题关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 8,8 | C. | 8,9 | D. | 18,8 |
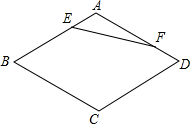 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF长度的范围是$\frac{\sqrt{3}}{2}$a≤EF≤a.
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF长度的范围是$\frac{\sqrt{3}}{2}$a≤EF≤a. 如图,在等腰直角三角形ABC中,∠ACB=90°,⊙C与AB相切于点D,若AB=4,则图中阴影部分的面积和为4-π.
如图,在等腰直角三角形ABC中,∠ACB=90°,⊙C与AB相切于点D,若AB=4,则图中阴影部分的面积和为4-π.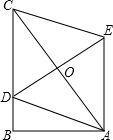 如图,在△ABC中,∠B=90°,AB=5,BC>AB,点D是BC上的动点,四边形ADCE是平行四边形,DE的最小值是5.
如图,在△ABC中,∠B=90°,AB=5,BC>AB,点D是BC上的动点,四边形ADCE是平行四边形,DE的最小值是5.