题目内容
18.阅读下面材料:在数学课上,老师提出如下问题:

小凯的作法如下:
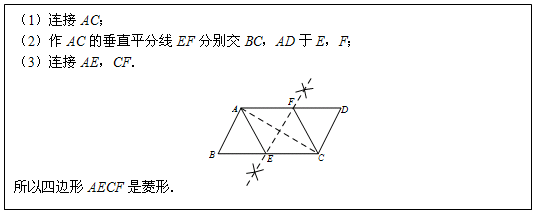
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是对角线互相垂直的平行四边形是菱形或有一组邻边相等的平行四边形是菱形或四条边都相等的四边形是菱形.
分析 利用线段垂直平分线的性质得到FA=FC,EA=EC,再证明四边形AECF为平行四边形,然后根据菱形的判定方法可判断四边形AECF是菱形.
解答 解:由作法得EF垂直平分AC,则FA=FC,EA=EC,再证明四边形AECF为平行四边形,从而得到四边形AECF为菱形,也可以证明四边相等得到四边形AECF为菱形.
故答案为对角线互相垂直的平行四边形是菱形或有一组邻边相等的平行四边形是菱形或四条边都相等的四边形是菱形.
点评 本题考查了作图-复杂作图、也考查了平行四边形和菱形的判定,解题的关键是灵活运用所学知识解决问题,注意本题答案不唯一.

练习册系列答案
相关题目
7. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 8,8 | C. | 8,9 | D. | 18,8 |
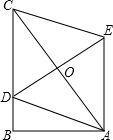 如图,在△ABC中,∠B=90°,AB=5,BC>AB,点D是BC上的动点,四边形ADCE是平行四边形,DE的最小值是5.
如图,在△ABC中,∠B=90°,AB=5,BC>AB,点D是BC上的动点,四边形ADCE是平行四边形,DE的最小值是5.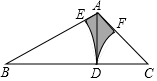 如图,在△ABC中,∠B=30°,∠C=45°,AD是BC边上的高,AB=4cm,分别以B、C为圆心,以BD、CD为半径画弧,交边AB、AC于点E、F,则图中阴影部分的面积是(2$\sqrt{3}$+2-$\frac{3}{2}$π)cm2.
如图,在△ABC中,∠B=30°,∠C=45°,AD是BC边上的高,AB=4cm,分别以B、C为圆心,以BD、CD为半径画弧,交边AB、AC于点E、F,则图中阴影部分的面积是(2$\sqrt{3}$+2-$\frac{3}{2}$π)cm2.