��Ŀ����
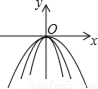
��ͼ��ʾ����ͬһƽ��ֱ������ϵ�У�������y=��3x2����y=��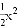 ����y=��x2��ͼ������ﵽ������������߶�Ӧ�ĺ���������______������ţ�
����y=��x2��ͼ������ﵽ������������߶�Ӧ�ĺ���������______������ţ�
 �� �� ��
����������y=?3x²����y=?x²����y=?x²��,������ϵ��a�ֱ�Ϊ?3��?��?1��
��|?3|>|?1|>���������ߢ�y=?x²�Ŀ������,�����ߢ�y=?3x²�Ŀ�����խ��
�ʴ�Ϊ���٢ۢڡ�
�� �� ��
����������y=?3x²����y=?x²����y=?x²��,������ϵ��a�ֱ�Ϊ?3��?��?1��
��|?3|>|?1|>���������ߢ�y=?x²�Ŀ������,�����ߢ�y=?3x²�Ŀ�����խ��
�ʴ�Ϊ���٢ۢڡ�
������y=x2��5x+6��x�ύ��A��B���㣬��AB�ij�Ϊ__��
 1
�������������������y=0����0=x2��5x+6��
��ã�x1=2��x2=3��
��AB�ij���3��2=1��
1
�������������������y=0����0=x2��5x+6��
��ã�x1=2��x2=3��
��AB�ij�Ϊ��3��2=1�� ��֪���������ε�һ����Ϊ75�㣬���䶥��Ϊ�� ��.
A. 30�� B. 75�� C. 105�� D. 30���75��
 D
�������������������Ϊ���������ε�һ����Ϊ75�㣬û����ȷ˵���ǵǻ��Ƕ��ǣ�����Ҫ������������з�����
��������
��75���Ϊ��ʱ������Ϊ180�㩁75���2=30�㣻
75���Ϊ����ʱ�����==52.5�㣬
�����䶥��Ϊ30���75�㣮
��ѡD��
D
�������������������Ϊ���������ε�һ����Ϊ75�㣬û����ȷ˵���ǵǻ��Ƕ��ǣ�����Ҫ������������з�����
��������
��75���Ϊ��ʱ������Ϊ180�㩁75���2=30�㣻
75���Ϊ����ʱ�����==52.5�㣬
�����䶥��Ϊ30���75�㣮
��ѡD�� ����1052��952�Ľ��Ϊ( )
A. 1000 B. 1980
C. 2000 D. 4000
 C
��������1052��952=��105+95����105-95��=200��10=2000����ѡC.
C
��������1052��952=��105+95����105-95��=200��10=2000����ѡC. ���κ���y=ax2+bx+c��ͼ���A����3��0����B��1��0����C��0��3������D�ں���ͼ���ϣ���C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ���ͼ�����B��D����
��1��һ�κ����Ͷ��κ����Ľ���ʽ��
��2��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
 ��1��y1=��x2��2x+3��2��x����2��x��1��
��������
�����������1����A��B��C��������������ߵĽ���ʽ�м�����ö��κ����Ľ���ʽ�������ɸ��������ߵĶԳ������D������꣬���ô���ϵ�������һ�κ�������ʽ��
��2�����ݣ�1����������ͼ����д��һ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
��������
��1�����κ���y1=ax2+bx+c��ͼ����A����3��0����...
��1��y1=��x2��2x+3��2��x����2��x��1��
��������
�����������1����A��B��C��������������ߵĽ���ʽ�м�����ö��κ����Ľ���ʽ�������ɸ��������ߵĶԳ������D������꣬���ô���ϵ�������һ�κ�������ʽ��
��2�����ݣ�1����������ͼ����д��һ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
��������
��1�����κ���y1=ax2+bx+c��ͼ����A����3��0����... ��֪�����ߵĽ���ʽΪy=��x-2��2+1�������������ߵĶ��������ǣ� ��.
A. ����2��1�� B. ��2��1�� C. ��2����1�� D. ��1��2��
 B
�����������ݶ���ʽy=��x-h��2+k�Ķ���Ϊ��h��k������y=��x-2��2+1Ϊ�����ߵĶ���ʽ����������Ϊ��2��1����
��ѡ��B��
B
�����������ݶ���ʽy=��x-h��2+k�Ķ���Ϊ��h��k������y=��x-2��2+1Ϊ�����ߵĶ���ʽ����������Ϊ��2��1����
��ѡ��B�� ��ͼ��ʾ�Ƕ��κ���y=ax2��x+a2��1��ͼ����a��ֵ�ǣ� ��
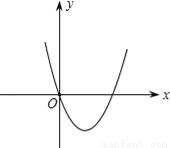
A. a=��1 B. a= C. a=1 D. a=1��a=��1
C. a=1 D. a=1��a=��1
 C
����������ͼ��ã��˶��κ�����ԭ�㣨0��0����
�ѵ㣨0��0�����뺯������ʽ��a2-1=0�����a=��1��
����Ϊ�˶��κ����Ŀ������ϣ�����a��0��
����a=1��
��ѡC��
C
����������ͼ��ã��˶��κ�����ԭ�㣨0��0����
�ѵ㣨0��0�����뺯������ʽ��a2-1=0�����a=��1��
����Ϊ�˶��κ����Ŀ������ϣ�����a��0��
����a=1��
��ѡC�� ��ƽ��ֱ������ϵ�У���������y=x2-4������ƽ��2����λ��������ƽ��2����λ���õ��������ߵĽ���ʽ�ǣ� ��
A. y=(x+2)2+2 B. y=(x-2)2-2 C. y=(x-2)2+2 D. y=(x+2)2-2
 B
��������������������ݶ��κ���ͼ������Ҽ����ϼ��¼���ƽ�ƹ��ɣ���֪����y=x2��4����ƽ��2����λ���ã�y=��x��2��2��4��������ƽ��2����λ���ã�y=��x��2��2��2��
��ѡB��
B
��������������������ݶ��κ���ͼ������Ҽ����ϼ��¼���ƽ�ƹ��ɣ���֪����y=x2��4����ƽ��2����λ���ã�y=��x��2��2��4��������ƽ��2����λ���ã�y=��x��2��2��2��
��ѡB�� �ڡ�ABCD�У���A����B�Ķ���֮��Ϊ5��4�����C���ڣ� ��
A. 60�� B. 80�� C. 100�� D. 120��
 C
���������������������Ĺؼ�����������ƽ���ı��ε��ڽǻ������Խ���ȣ�����ƽ���ı��ε����ʿɵá�A����B�������Ӷ�����á�A�Ķ��������ɵõ������
�ߡ�ABCD��
���A+��B =180�㣬
�ߡ�A����B�Ķ���֮��Ϊ5��4��
���C =��A=100�㣮
��ѡC��
C
���������������������Ĺؼ�����������ƽ���ı��ε��ڽǻ������Խ���ȣ�����ƽ���ı��ε����ʿɵá�A����B�������Ӷ�����á�A�Ķ��������ɵõ������
�ߡ�ABCD��
���A+��B =180�㣬
�ߡ�A����B�Ķ���֮��Ϊ5��4��
���C =��A=100�㣮
��ѡC�� 
