题目内容
已知等腰三角形的一个角为75°，则其顶角为（ ）.
A. 30° B. 75° C. 105° D. 30°或75°
D
【解析】试题分析：因为等腰三角形的一个角为75°，没有明确说明是底角还是顶角，所以要分两种情况进行分析．
【解析】
当75°角为底角时，顶角为180°﹣75°×2=30°；
75°角为顶角时，其底角==52.5°，
所以其顶角为30°或75°．
故选D．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
。
【解析】试题分析：根据矩形的性质得∠B=∠D=∠BAD=90°，根据旋转的性质得∠D′=∠D=90°，∠4=α，利用对顶角相等得到∠1=∠2=110°，再根据四边形的内角和为360°可计算出∠3=70°，然后利用互余即可得到∠α的度数．
【解析】
如图，
∵四边形ABCD为矩形，
∴∠B=∠D=∠BAD=90°，
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′... 如图，等边三角形ABD和等边三角形CBD的边长均为a，现把它们拼合起来，E是AD上异于A、D两点的一动点，F是CD上一动点，满足AE+CF=a．则△BEF的形状如何？
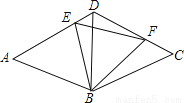
△BEF为正三角形，理由见解析
【解析】试题分析：根据已知条件易证△BDE≌△BCF，即可求得∠FBD+∠DBE=60°，根据一个内角为60°的等腰三角形可以判定为等边三角形，即可得结论．
试题解析：
△BEF为正三角形
证明：∵AE+CF=a，AE+ED=a，
∴DE=CF，
在△BDE和△BCF中，
∴△BDE≌△BCF，
∴BE=BF，∠CBF... 每一个多边形都可以按图的方法割成若干个三角形．而每一个三角形的三个内角的和是180°．按图的方法，十二边形的内角和是__________度．
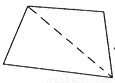
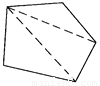
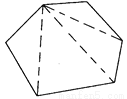
1800
【解析】∵过四边形的一个顶点可画一条对角线，将四边形分成两个三角形，
过五边形的一个顶点可画两条对角线，将五边形分成三个三角形，
过六边形的一个顶点可画三条对角线，将六边形分成四个三角形，
∴过十二边形的一个顶点可画九条对角线，将十二边形分成十个三角形，
而三角形的内角和等于180°，
∴十二边形的内角和是180°×10=1800°.
故答案为：... 过△ABC的顶点C作边AB的垂线将∠ACB分为20°和40°的两个角，那么∠A，∠B中较大的角的度数是____________．
70°
【解析】根据题意画出图形，则∠ACD=40°，∠DCB=20°.
∵CD⊥AB，∠ACD=40°，∠DCB=20°，
∴∠A=50°，∠B=70°，
∴∠A、∠B中较大的角的度数是70°.
故答案为：70°. 在锐角三角形中，最大角α的取值范围是 ( )
A. 0°＜α＜90° B. 60°＜α＜90° C. 60°＜α＜180° D. 60°≤α＜90°
D
【解析】三角形三个内角的和等于180°，设其他两个角分别为β和γ，由题意α<90°，α?β且α?γ，α+β+γ=180°，所以3α?180°，即α?60°.
故选：D. 分解因式：4m3n－16mn3.
4mn(m＋2n)(m－2n)
【解析】试题分析：提取公因式4mn后，再利用平方差公式因式分解即可.
试题解析：
4m3n－16mn3
=4mn(m2－4n2)
=4mn(m＋2n)(m－2n). 如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣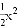
，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）
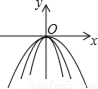
① ③ ②
【解析】①y=?3x²，②y=?x²，③y=?x²中,二次项系数a分别为?3、?、?1，
∵|?3|>|?1|>，∴抛物线②y=?x²的开口最宽,抛物线①y=?3x²的开口最窄。
故答案为：①③②。 (1)解不等式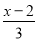
－
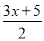≥x－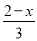
，并把它的解集在数轴上表示出来．
(2)解不等式组： 
，并把解集在数轴上表示出来．
（1）x≤－1，解集在数轴上表示见解析；（2）原不等式组无解.
【解析】试题分析：（1）根据不等式的解法，利用去分母，去括号，移项合并同类项，系数化为1，解不等式，再表示在数轴上即可；
（2）分别解两个不等式，然后求出不等式组的解集，并表示在数轴上.
试题解析：(1) 【解析】
原不等式化简为：2x－4－9x－15≥6x－4＋2x，解得x≤－1，解集在数轴上表示为：
(2...