题目内容
抛物线y=x2﹣5x+6与x轴交于A、B两点，则AB的长为__．
1
【解析】试题分析：当y=0，则0=x2﹣5x+6，
解得：x1=2，x2=3，
故AB的长为：3﹣2=1．
练习册系列答案
相关题目
用十个球设计一个游戏，使摸到红球、白球的可能性相同，并且摸到黄球的可能性比摸到红球的可能性小．
红球4个，白球4个，黄球2个.
【解析】试题分析：此题要想使摸到红球、白球的可能性相同，摸到黄球的可能性比摸到红球的可能性小，只要红球、白球个数相同，红球的个数多于黄球的个数即可．
试题解析：由题意知共10个球，即红球个数+白球个数+黄球个数＝10
摸到红球、白球的可能性相同
∴红球个数=白球个数=1，2，3，4
∴红球个数，白球个数，黄球个数可能是:1，1，8或2，... 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
。
【解析】试题分析：根据矩形的性质得∠B=∠D=∠BAD=90°，根据旋转的性质得∠D′=∠D=90°，∠4=α，利用对顶角相等得到∠1=∠2=110°，再根据四边形的内角和为360°可计算出∠3=70°，然后利用互余即可得到∠α的度数．
【解析】
如图，
∵四边形ABCD为矩形，
∴∠B=∠D=∠BAD=90°，
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′... 将长度为5cm的线段向上平移10cm所得线段长度是（ ）
A. 10cm B. 5cm C. 0cm D. 无法确定
B
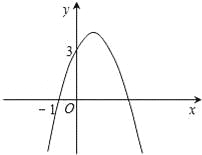
【解析】平移不改变图形的大小和形状．故线段长度不变，仍为5cm． 已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）．
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围．
（1）b="2,c=3," y=﹣x2+2x+3．(2) ﹣1＜x＜3
【解析】试题分析：（1）把抛物线上的两点代入解析式，解方程组可求b、c的值；
（2）令y=0，求抛物线与x轴的两交点坐标，观察图象，求y＞0时，x的取值范围．
试题解析：（1）将点（﹣1，0），（0，3）代入y=﹣x2+bx+c中，得
，解得．
∴y=﹣x2+2x+3．
（2）令y=0，解方... 根据下列表格对应值：
x | 3 | 4 | 5 |
y=ax2+bx+c | 0.5 | ﹣0.5 | ﹣1 |
判断关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是（ ）
A. x＜3 B. x＞5 C. 3＜x＜4 D. 4＜x＜5
C
【解析】试题分析：∵x=3时，y=0.5，即ax2+bx+c＞0；
x=4时，y=﹣0.5，即ax2+bx+c＜0，
∴抛物线与x轴的一个交点在（3，0）和（4，0）之间，
∴关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是3＜x＜4．
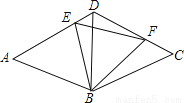
故选C． 如图，等边三角形ABD和等边三角形CBD的边长均为a，现把它们拼合起来，E是AD上异于A、D两点的一动点，F是CD上一动点，满足AE+CF=a．则△BEF的形状如何？
△BEF为正三角形，理由见解析
【解析】试题分析：根据已知条件易证△BDE≌△BCF，即可求得∠FBD+∠DBE=60°，根据一个内角为60°的等腰三角形可以判定为等边三角形，即可得结论．
试题解析：
△BEF为正三角形
证明：∵AE+CF=a，AE+ED=a，
∴DE=CF，
在△BDE和△BCF中，
∴△BDE≌△BCF，
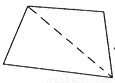
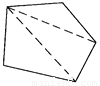
∴BE=BF，∠CBF... 每一个多边形都可以按图的方法割成若干个三角形．而每一个三角形的三个内角的和是180°．按图的方法，十二边形的内角和是__________度．
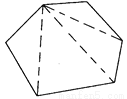
1800
【解析】∵过四边形的一个顶点可画一条对角线，将四边形分成两个三角形，
过五边形的一个顶点可画两条对角线，将五边形分成三个三角形，
过六边形的一个顶点可画三条对角线，将六边形分成四个三角形，
∴过十二边形的一个顶点可画九条对角线，将十二边形分成十个三角形，
而三角形的内角和等于180°，
∴十二边形的内角和是180°×10=1800°.
故答案为：... 如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣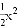
，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）
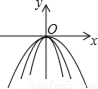
① ③ ②
【解析】①y=?3x²，②y=?x²，③y=?x²中,二次项系数a分别为?3、?、?1，
∵|?3|>|?1|>，∴抛物线②y=?x²的开口最宽,抛物线①y=?3x²的开口最窄。
故答案为：①③②。