题目内容
计算1052－952的结果为( )
A. 1000 B. 1980
C. 2000 D. 4000
C
【解析】1052－952=（105+95）（105-95）=200×10=2000，故选C.
练习册系列答案
相关题目
将长度为5cm的线段向上平移10cm所得线段长度是（ ）
A. 10cm B. 5cm C. 0cm D. 无法确定
B
【解析】平移不改变图形的大小和形状．故线段长度不变，仍为5cm． 每一个多边形都可以按图的方法割成若干个三角形．而每一个三角形的三个内角的和是180°．按图的方法，十二边形的内角和是__________度．
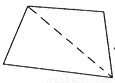
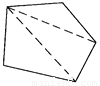
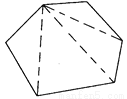
1800
【解析】∵过四边形的一个顶点可画一条对角线，将四边形分成两个三角形，
过五边形的一个顶点可画两条对角线，将五边形分成三个三角形，
过六边形的一个顶点可画三条对角线，将六边形分成四个三角形，
∴过十二边形的一个顶点可画九条对角线，将十二边形分成十个三角形，
而三角形的内角和等于180°，
∴十二边形的内角和是180°×10=1800°.
故答案为：... 在锐角三角形中，最大角α的取值范围是 ( )
A. 0°＜α＜90° B. 60°＜α＜90° C. 60°＜α＜180° D. 60°≤α＜90°
D
【解析】三角形三个内角的和等于180°，设其他两个角分别为β和γ，由题意α<90°，α?β且α?γ，α+β+γ=180°，所以3α?180°，即α?60°.
故选：D. 分解因式：4m3n－16mn3.
4mn(m＋2n)(m－2n)
【解析】试题分析：提取公因式4mn后，再利用平方差公式因式分解即可.
试题解析：
4m3n－16mn3
=4mn(m2－4n2)
=4mn(m＋2n)(m－2n). 如图，抛物线y=﹣x2+3x+4与x轴交于点A，B，与y轴交于点C，P（m，n）为第一象限内抛物线上的一点，点D的坐标为（0，6）．
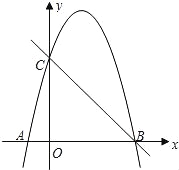
（1）OB=_________，抛物线的顶点坐标为_________________；
（2）当n=4时，求点P关于直线BC的对称点P′的坐标；
（3）是否存在直线PD，使直线PD所对应的一次函数随x的增大而增大？若存在，直接写出m的取值范围；若不存在，请说明理由．
（1）4，（，）；（2）（0，1）；（3）1＜m＜2．
【解析】
试题分析：（1）当y=0时，即﹣x2+3x+4=0，解得：x1=4，x2=﹣1，∴点A（﹣1，0）点B（4，0），∴OB=4，y=﹣x2+3x+4=，∴抛物线的顶点坐标为（，），故答案为：4，（，）．
（2）如图，连接CP，CP′，
n=4时，﹣m2+3m+4=4，解得：m1=3，m2=0（舍去），∴这时P点... 如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣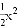
，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）
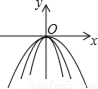
① ③ ②
【解析】①y=?3x²，②y=?x²，③y=?x²中,二次项系数a分别为?3、?、?1，
∵|?3|>|?1|>，∴抛物线②y=?x²的开口最宽,抛物线①y=?3x²的开口最窄。
故答案为：①③②。 已知二次函数的图象经过点（0，﹣3），且顶点坐标为（﹣1，﹣4）．
（1）求该二次函数的解析式；
（2）设该二次函数的图象与x轴的交点为A、B，与y轴的交点为C，求△ABC的面积．
1.【解析】
（1）设，把点代入得：-----------2分
∴函数解析式或-----------------------------2分
2.（2）∵，解得，
∴，，。---------（2分）
∴△ABC的面积=。--------------------------（2分）
【解析】试题分析：（1）先设所求函数解析式是y=a（x+1）2﹣4，再把（0，﹣3）代... 在△ABC中，AB＝8 ㎝，AC＝10 ㎝，P，G，H分别是AB，BC，CA的中点，则四边形APGH的周长是______ ．
18cm
【解析】【解析】
∵P、G、H分别是AB、BC、CA的中点，∴PG、HG为△ABC的中位线，∴AP=AB=×8=4cm，AH=AC=×10=5cm，∴PG∥AC，GH∥AB，∴四边形APGH为平行四边形，HG=AP=4cm，PG=AH=5cm，∴四边形APGH的周长是（4+5）×2=18cm．
故答案为：18cm．