题目内容
二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：
（1）一次函数和二次函数的解析式；
（2）写出使一次函数值大于二次函数值的x的取值范围．
（1）y1=﹣x2﹣2x+3（2）x＜﹣2或x＞1．
【解析】
试题分析：（1）将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式，进而可根据抛物线的对称轴求出D点的坐标，再用待定系数法求出一次函数解析式；
（2）根据（1）画出函数图象，即可写出一次函数值大于二次函数值的x的取值范围．
【解析】
（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），...
练习册系列答案
口算题天天练系列答案
相关题目
已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）．
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围．
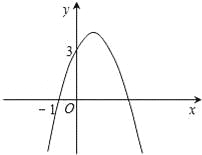
（1）b="2,c=3," y=﹣x2+2x+3．(2) ﹣1＜x＜3
【解析】试题分析：（1）把抛物线上的两点代入解析式，解方程组可求b、c的值；
（2）令y=0，求抛物线与x轴的两交点坐标，观察图象，求y＞0时，x的取值范围．
试题解析：（1）将点（﹣1，0），（0，3）代入y=﹣x2+bx+c中，得
，解得．
∴y=﹣x2+2x+3．
（2）令y=0，解方... 过△ABC的顶点C作边AB的垂线将∠ACB分为20°和40°的两个角，那么∠A，∠B中较大的角的度数是____________．
70°
【解析】根据题意画出图形，则∠ACD=40°，∠DCB=20°.
∵CD⊥AB，∠ACD=40°，∠DCB=20°，
∴∠A=50°，∠B=70°，
∴∠A、∠B中较大的角的度数是70°.
故答案为：70°. 分解因式：4m3n－16mn3.
4mn(m＋2n)(m－2n)
【解析】试题分析：提取公因式4mn后，再利用平方差公式因式分解即可.
试题解析：
4m3n－16mn3
=4mn(m2－4n2)
=4mn(m＋2n)(m－2n). 分解因式：16－x2＝( )
A. (4－x)(4＋x) B. (x－4)(x＋4)
C. (8＋x)(8－x) D. (4－x)2
A
【解析】试题分析：直接利用平方差公式分解因式得出答案．16﹣x2=（4﹣x）（4+x）． 如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣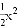
，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）
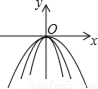
① ③ ②
【解析】①y=?3x²，②y=?x²，③y=?x²中,二次项系数a分别为?3、?、?1，
∵|?3|>|?1|>，∴抛物线②y=?x²的开口最宽,抛物线①y=?3x²的开口最窄。
故答案为：①③②。 如图，小姚身高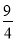
m在某次投篮中，球的运动路线是抛物线
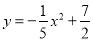的一部分，若命中篮圈中心，则他与篮底的距离
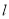是（ ）
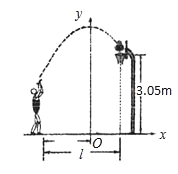
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：分别求出当y=3.05和当y=时的x的值，前面那个取正数，后面的那个取负数，然后计算它们之间的距离. 已知点P（-1，m）在二次函数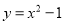
的图象上，则m的值为____________；
0
【解析】∵点P（-1，m）在二次函数y=x2-1的图象上，
∴m=1-1=0．
故答案是：0． 如图所示，梯形ABCD中AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A′处，若∠A′BC＝20°，则∠A′BD的度数为（ ）
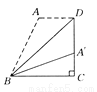
A. 15° B. 20° C. 25° D. 30°
C
【解析】∵∠A′BC=20°
∴∠BA′C=70°
∴∠DA′B=110°
∴∠DAB=110°
∴∠ABC=70°
∴∠ABA′=∠ABC﹣∠A′BC=70°﹣20°=50°
∴∠A′BD=∠ABA′=25°．
故选C．