题目内容
14.如图是用棋子按一定规律摆成的图形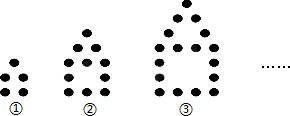
(1)观察图形,填写下表:
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
(3)是否存在一个图形,使其中含棋子的个数为100?不存在(填(“存在”或“不存在”)
分析 (1)(2)由题意可知:第①个图形需要1+1×4=5个棋子,第②个图形需要3+2×4=11个棋子,第③个图形需要5+3×4=17个棋子,…由此得出第n个图形需要2n-1+4n=(6n-1)个棋子;
(3)由题意列出方程求得方程的解判定即可.
解答 解:(1)填表如下:
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
(3)由题意可知:6n-1=100,
解得:n=$\frac{101}{6}$,
∵n为整数,
∴不存在一个图形,使其中含棋子的个数为100.
故答案为:(1)5,11,17,23;(2)(6n-1);(3)不存在.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
4. 如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
 如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )| A. | 60° | B. | 90° | C. | 105° | D. | 120° |
6.同时经过平面三点可确定的直线的条数是( )
| A. | 0 | B. | 0或1 | C. | 1或3 | D. | 3 |
4.等腰三角形的两边分别为12和6,则这个三角形的周长是( )
| A. | 24 | B. | 18 | C. | 30 | D. | 24或30 |
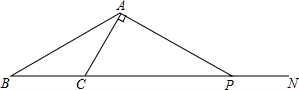 如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.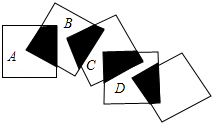 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是9cm2.
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是9cm2.

