题目内容
4．
如图，在⊙O中，弦AC、BD交于点E，弧AB=弧BC=弧CD．若∠BDC=25°，则∠ACD等于（ ）| A． | 60° | B． | 90° | C． | 105° | D． | 120° |
分析 先根据∠BDC=25°求出弧AB=弧BC=弧CD的度数，进而可得出优弧AD的度数，由圆周角与弧的关系即可得出结论．
解答 解：∵∠BDC=25°，
∴弧AB=弧BC=弧CD=50°，
∴优弧AD=360°-3×50°=210°，
∴∠ACD=$\frac{1}{2}$×210°=105°．
故选C．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
如图，△ACE，△ABF都是等腰直角三角形．∠BAF=∠CAE=90°．那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合．
9．已知α为锐角，则sinα的值不可能为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{3}$ | D． | 2 |
14．如图是用棋子按一定规律摆成的图形
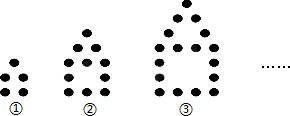
（1）观察图形，填写下表：
（2）按照这种规律摆下去，第n个图形需要（6n-1）个棋子；
（3）是否存在一个图形，使其中含棋子的个数为100？不存在（填（“存在”或“不存在”）
（1）观察图形，填写下表：
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
（3）是否存在一个图形，使其中含棋子的个数为100？不存在（填（“存在”或“不存在”）