题目内容
2．
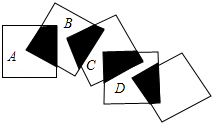将五个边长都为3cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和是9cm2．
分析 根据正方形的中心对称性，得到每一个阴影部分的面积等于正方形面积的$\frac{1}{4}$，四块阴影面积的总和正好等于一个正方形的面积，然后列式计算即可．
解答 解：由中心对称的性质和正方形的性质得，一个阴影部分的面积等于正方形的面积的$\frac{1}{4}$，
所以，四块阴影面积的总和正好等于一个正方形的面积，
∵五个正方形的边长都为3cm，
∴四块阴影面积的总和为9（cm2），
故答案为：9．
点评 本题考查了中心对称和正方形的性质，熟记中心对称性的性质、判断出每一个阴影部分的面积等于正方形的面积的$\frac{1}{4}$是解题的关键．
练习册系列答案
相关题目
17．某校开展“文明小卫士”活动，从学生会“督查部”的3名学生（2男1女）中随机选两名进行督导，恰好选中两名男学生的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
7．
有理数a、b在数轴上的位置如图所示，则-a与b的大小关系是（ ）
有理数a、b在数轴上的位置如图所示，则-a与b的大小关系是（ ）| A． | -a＞b | B． | -a=b | C． | -a＜b | D． | 不能判断 |
14．如图是用棋子按一定规律摆成的图形
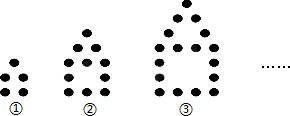
（1）观察图形，填写下表：
（2）按照这种规律摆下去，第n个图形需要（6n-1）个棋子；
（3）是否存在一个图形，使其中含棋子的个数为100？不存在（填（“存在”或“不存在”）
（1）观察图形，填写下表：
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
（3）是否存在一个图形，使其中含棋子的个数为100？不存在（填（“存在”或“不存在”）