题目内容
19.如图,是一个正三棱柱的三视图,求这个三棱柱的表面积和体积.
分析 画出几何体的图形,通过三视图的数据说明几何体的棱长,然后利用表面积与体积公式求解即可.
解答 解:由三视图易知,该正三棱柱的形状如图所示:
且AA′=BB′=CC′=4cm,
正三角形ABC和正三角形A′B′C′的高为2$\sqrt{3}$ cm.
∴正三角形ABC的边长为AB=4.
∴该三棱柱的表面积为
S=3×4×4+2×$\frac{1}{2}$×42sin60°=48+8 $\sqrt{3}$(cm2),
体积为V=S底•AA′=$\frac{1}{2}$×42sin60°×4=16 $\sqrt{3}$(cm3).
故这个三棱柱的表面积为(48+8$\sqrt{3}$)cm2,体积为16$\sqrt{3}$cm3.
点评 本题考查几何体的三视图复原几何体以及几何体的表面积与体积的求法,同时也考查了学生空间想象能力与计算能力.能够由三视图得到几何体的立体图是解题关键.

练习册系列答案
相关题目
9.已知α为锐角,则sinα的值不可能为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
7. 有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )
有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )
 有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )
有理数a、b在数轴上的位置如图所示,则-a与b的大小关系是( )| A. | -a>b | B. | -a=b | C. | -a<b | D. | 不能判断 |
14.如图是用棋子按一定规律摆成的图形
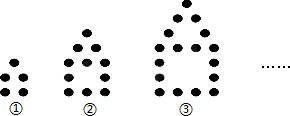
(1)观察图形,填写下表:
(2)按照这种规律摆下去,第n个图形需要(6n-1)个棋子;
(3)是否存在一个图形,使其中含棋子的个数为100?不存在(填(“存在”或“不存在”)

(1)观察图形,填写下表:
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
(3)是否存在一个图形,使其中含棋子的个数为100?不存在(填(“存在”或“不存在”)
 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.若△ACP为等腰三角形,在图中作出所有符合条件的点P,要求:
如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.若△ACP为等腰三角形,在图中作出所有符合条件的点P,要求: 如图,在△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,求△ABC的周长.
如图,在△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,求△ABC的周长. 如图,直线l是一条河,P,Q两地在直线l的同侧,欲在l上的某点M处修建一个水泵站,分别向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的方案是( )
如图,直线l是一条河,P,Q两地在直线l的同侧,欲在l上的某点M处修建一个水泵站,分别向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的方案是( )


