题目内容
9.如图,已知△ABC是等边三角形.(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.

分析 (1)猜想:AB=AF+BD;
(2)猜想:AB=AF-BD;
(3)过点E作EG∥BC交AC于点G,得△AEG为等边三角形,证明△BDE≌△GEC,得到BD=EG=AE又因为AF=BE,所以AB=BE+AE=AF+BD.
解答 解:(1)猜想:AB=AF+BD;
(2)如图2,猜想:AB=AF-BD; 
(3)如图(1),过点E作EG∥BC交AC于点G,得△AEG为等边三角形,
∵DE=CE,
∴∠CDE=∠ECD,
又∵∠CDE+∠BED=∠ABC=∠ACD=∠ECD+∠GCE,
∴∠BED=∠GCE,
在△BDE和△GEC中,
$\left\{\begin{array}{l}{ED=EC}\\{∠BED=∠GCE}\\{BE=CG}\end{array}\right.$,
∴△BDE≌△GEC,
∴BD=EG=AE
又∵AF=BE,
∴AB=BE+AE=AF+BD.
点评 本题考查了全等三角形的判定和性质的应用,解决本题的关键是利用数形结合,作出辅助线,证明三角形全等.

练习册系列答案
相关题目
17.某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
14.如图是用棋子按一定规律摆成的图形
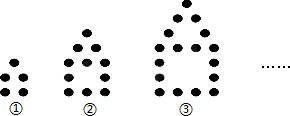
(1)观察图形,填写下表:
(2)按照这种规律摆下去,第n个图形需要(6n-1)个棋子;
(3)是否存在一个图形,使其中含棋子的个数为100?不存在(填(“存在”或“不存在”)

(1)观察图形,填写下表:
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
(3)是否存在一个图形,使其中含棋子的个数为100?不存在(填(“存在”或“不存在”)
18.方程x2=9的解是( )
| A. | x1=x2=3 | B. | x1=x2=9 | C. | x1=3,x2=-3 | D. | x1=9,x2=-9 |

 如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=7cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距5cm?
如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=7cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距5cm?