题目内容
4．等腰三角形的两边分别为12和6，则这个三角形的周长是（ ）| A． | 24 | B． | 18 | C． | 30 | D． | 24或30 |
分析 本题没有明确说明已知的边长哪个是腰长，则有两种情况：①腰长为6；②腰长为12．再根据三角形的性质：三角形的任意两边的和＞第三边，任意两边之差＜第三边判断是否满足，再将满足的代入周长公式即可得出周长的值．
解答 解：（1）当三边是6cm，6cm，12cm时，6+6=12cm，不符合三角形的三边关系，应舍去；
（2）当三边是6cm，12cm，12cm时，符合三角形的三边关系，此时周长是30cm；
所以这个三角形的周长是30cm．
故选C．
点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
14．如图是用棋子按一定规律摆成的图形
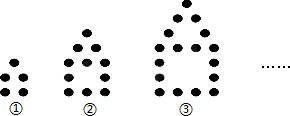
（1）观察图形，填写下表：
（2）按照这种规律摆下去，第n个图形需要（6n-1）个棋子；
（3）是否存在一个图形，使其中含棋子的个数为100？不存在（填（“存在”或“不存在”）
（1）观察图形，填写下表：
| 图形 | ① | ② | ③ | ④ |
| 棋子个数 | 5 | 11 | 17 | 23 |
（3）是否存在一个图形，使其中含棋子的个数为100？不存在（填（“存在”或“不存在”）
如图，直线l是一条河，P，Q两地在直线l的同侧，欲在l上的某点M处修建一个水泵站，分别向P，Q两地供水．现有如下四种铺设方案，则铺设的管道最短的方案是（ ）
16．
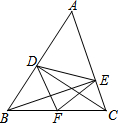如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE=5，BC=8，则△DEF的周长是（ ）
如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE=5，BC=8，则△DEF的周长是（ ）| A． | 21 | B． | 18 | C． | 13 | D． | 15 |
如图，△ABC中，点D在边AB上，AC=BC=BD，AD=CD，求∠A的度数．