题目内容
14．在平面直角坐标系中，已知点A（-4，2），B（-6，-4），以原点O为位似中心，在原点的同一旁，把△ABO缩小，相似比为$\frac{1}{2}$，则点A的对应点A′的坐标是（ ）| A． | （-2，1） | B． | （-8，4） | C． | （-4，1） | D． | （-2，2） |
分析 利用位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，把A点的横纵坐标分别乘以$\frac{1}{2}$即可得到点A的对应点A′的坐标．
解答 解：点A（-4，2）的对应点A′的坐标是（-2，1）．
故选A．
点评 本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．
练习册系列答案
相关题目
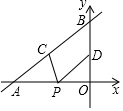如图，直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（-$\frac{3}{2}$，0）．
已知△ABC如图所示，A（-4，1），B（-1，1），C（-4，3），在网格中按要求画图：
19．抛物线y=-2（x-1）2上有三点A（-1，y1），B（$\sqrt{2}$，y2），C（2，y3），则y1，y2，y3 从小到大是（ ）
| A． | y1＜y2＜y3 | B． | y2＜y3＜y1 | C． | y2＜y1＜y3 | D． | y1＜y3＜y2 |