题目内容
3.在等腰△ABC中,腰长AB=5,底边BC=6,则△ABC的面积为12.分析 根据题意画出图形,利用三线合一得到BD的长,在直角三角形ABD中,利用勾股定理即可求出AD的长,即可求出三角形的面积.
解答  解:如图所示,作AD⊥BC于D,
解:如图所示,作AD⊥BC于D,
∵AB=AC=5,AD⊥BC,BC=6,
∴BD=CD=$\frac{1}{2}$BC=3,
在Rt△ABD中,根据勾股定理得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4.
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×4=12.
故答案为:12.
点评 此题考查的是勾股定理及等腰三角形的性质;熟练掌握等腰三角形的性质,由勾股定理求出AD是解答此题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
14.在平面直角坐标系中,已知点A(-4,2),B(-6,-4),以原点O为位似中心,在原点的同一旁,把△ABO缩小,相似比为$\frac{1}{2}$,则点A的对应点A′的坐标是( )
| A. | (-2,1) | B. | (-8,4) | C. | (-4,1) | D. | (-2,2) |
18. 如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
 如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.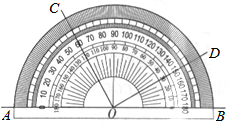 如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
 如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
如图所示,用量角器度量一些角的度数.下列结论中正确的是( )| A. | ∠BOC=60° | B. | ∠COD=150° | ||
| C. | ∠AOC与∠BOD的大小相等 | D. | ∠AOC与∠BOD互余 |
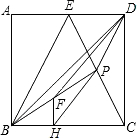 如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH.
如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH.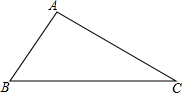 如图,在△ABC中,∠B=55°,∠C=30°.
如图,在△ABC中,∠B=55°,∠C=30°.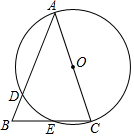 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.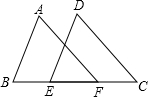 如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).
如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).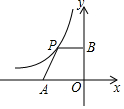 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )