题目内容
6.先化简,再求式子(1-$\frac{1}{a+2}$)÷$\frac{{a}^{2}-1}{a+2}$的值,其中a=-5+(-2017)0.分析 先算括号里面的,再把分子分母因式分解,约分即可,把a化简,再代入计算即可.
解答 解:原式=($\frac{a+2}{a+2}$-$\frac{1}{a+2}$)•$\frac{a+2}{(a+1)(a-1)}$
=$\frac{a+1}{a+2}$•$\frac{a+2}{(a+1)(a-1)}$
=$\frac{1}{a-1}$,
当a=-5+(-2017)0=-5+1=-4时,
原式=$\frac{1}{a-1}$=$\frac{1}{-4-1}$=-$\frac{1}{5}$.
点评 本题考查了分式的化简求值以及零指数幂运算,还涉及因式分解,通分、约分,掌握运算法则是解题的关键.

练习册系列答案
相关题目
16. 如图,D是BC上一点,E是AB上一点,AD、CE交于点P,且AE:EB=3:2,CP:CE=5:6,那么DB:CD=( )
如图,D是BC上一点,E是AB上一点,AD、CE交于点P,且AE:EB=3:2,CP:CE=5:6,那么DB:CD=( )
 如图,D是BC上一点,E是AB上一点,AD、CE交于点P,且AE:EB=3:2,CP:CE=5:6,那么DB:CD=( )
如图,D是BC上一点,E是AB上一点,AD、CE交于点P,且AE:EB=3:2,CP:CE=5:6,那么DB:CD=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:4 |
14.在平面直角坐标系中,已知点A(-4,2),B(-6,-4),以原点O为位似中心,在原点的同一旁,把△ABO缩小,相似比为$\frac{1}{2}$,则点A的对应点A′的坐标是( )
| A. | (-2,1) | B. | (-8,4) | C. | (-4,1) | D. | (-2,2) |
18. 如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
 如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
16.二次函数y=2(x-3)2+5的图象的顶点坐标为( )
| A. | (3,5) | B. | (3,-5) | C. | (-3,5) | D. | (-3,-5) |
 如图,△ABC是一块铁皮余料.已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图,△ABC是一块铁皮余料.已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.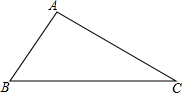 如图,在△ABC中,∠B=55°,∠C=30°.
如图,在△ABC中,∠B=55°,∠C=30°.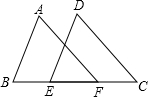 如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).
如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).