题目内容
19.抛物线y=-2(x-1)2上有三点A(-1,y1),B($\sqrt{2}$,y2),C(2,y3),则y1,y2,y3 从小到大是( )| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y2<y1<y3 | D. | y1<y3<y2 |
分析 根据二次函数的性质求出抛物线的对称轴,根据二次函数的增减性解答.
解答 解:∵抛物线y=-2(x-1)2的对称轴是x=1,
∴x=-1时的函数值与x=3时的函数值相等,当x>1时,y随x的增大而减小,
∵$\sqrt{2}$<2<3,
∴y1<y3<y2,
故选:D.
点评 本题考查的是二次函数图象上点的坐标特征,掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
7.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=-$\frac{5}{2}$t2+20t+1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
| A. | 3 s | B. | 4 s | C. | 5 s | D. | 6 s |
14.在平面直角坐标系中,已知点A(-4,2),B(-6,-4),以原点O为位似中心,在原点的同一旁,把△ABO缩小,相似比为$\frac{1}{2}$,则点A的对应点A′的坐标是( )
| A. | (-2,1) | B. | (-8,4) | C. | (-4,1) | D. | (-2,2) |
9.若a<0,b>0,化简|a|+|2b|-|a-b|得( )
| A. | b | B. | -b | C. | -3b | D. | 2a+b |
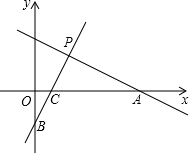 如图,已知直线y=ax-1与x轴和y轴分别交于C、B两点,直线y=-$\frac{2}{3}$x+b与x轴交于A,并且这两条直线交于P(2,2).
如图,已知直线y=ax-1与x轴和y轴分别交于C、B两点,直线y=-$\frac{2}{3}$x+b与x轴交于A,并且这两条直线交于P(2,2).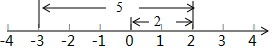 如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照图并思考,完成下列各题.
如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照图并思考,完成下列各题.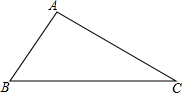 如图,在△ABC中,∠B=55°,∠C=30°.
如图,在△ABC中,∠B=55°,∠C=30°.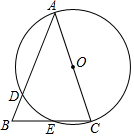 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.