题目内容
7.【问题情境】数学课上,李老师提出了如下问题:在△ABC中,∠ABC=∠ACB=α,点D是AB边上任意一点,将射线DC绕点D逆时针旋转α与过点A且平行于BC边的直线交于点E.请判断线段BD与AE之间的数量关系.
小颖在小组合作交流中,发表自己的意见:“我们不妨从特殊情况下获得解决问题的思路,然后类比到一般情况.”小颖的想法获得了其他成员一致的赞成.
【问题解决】
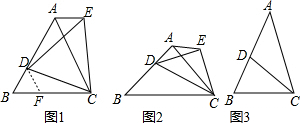
如图1,当α=60°时,判断BD与AE之间的数量关系.
解法如下:过D点作AC的平行线交BC于F,构造全等三角形,通过推理使问题得到解决,请你直接写出线段BD与AE之间的数量关系:BD=AE.
【类比探究】
(2)如图2,当α=45°时,请判断线段BD与AE之间的数量关系,并进行证明;
(3)如图3,当α为任意锐角时,请直接写出线段BD与AE之间的数量关系:BD=2cosα•AE.(用含α的式子表示,其中0°<α<90°)
分析 【问题情境】可利用四点共圆证角相等,然后证△BDC∽△AEC相似可以确定BD=2cosα•AE.
【问题解决】当α=60°时,△ABC、△DCE是等边三角形,EC=DC,AC=BC,根据等量减等量求得∠BCD=∠ACE,可得△BDC≌△ACE,答案可证.
【类比探究】(2)过点D作DF∥AC,交BC于F,可证得△DFB是等腰直角三角形,BD=DF=$\sqrt{2}$BF,再证明△ADE∽△FCD,得$\frac{AE}{DF}=\frac{AD}{CF}$,由DF∥AC,得$\frac{BD}{BF}=\frac{AD}{CF}$.得出$\frac{AE}{BD}=\frac{BD}{BF}$=$\frac{\sqrt{2}}{2}$.即可得出结论.
(3)可利用四点共圆证角相等,然后证△BDC∽△AEC相似可以确定BD=2cosα•AE.
解答 【问题情境】解:BD=2cosα•AE;理由如下:∵AE∥BC,∠EAC=∠ACB=α,
∴∠EAC=∠EDC=α,
∴A、D、C、E四点共圆,
∴∠ADE=∠ACE,
∵∠ADE+∠EDC=∠ADC=∠ABC+∠BCD,∠ABC=∠EDC=α,
∴∠ADE=∠BCD,
∴∠ACE=∠BCD
∵∠ABC=∠EAC=α,
∴△BDC∽△ACE,
∴$\frac{BD}{AE}=\frac{BC}{AC}$,
又∵$\frac{BC}{AC}$=2cosα,∴BD=2cosα•AE.
故答案为BD=2cosα•AE.
【问题解决】解:当α=60°时,△ABC、△DCE是等边三角形,
∴EC=DC,AC=BC,∠ACB=∠DCE=60°,
∴∠ACB-∠ACD=∠DCE-∠ACD,
即∠BCD=∠ACE,
在△BDC和△ACE中,$\left\{\begin{array}{l}{EC=DC}&{\;}\\{∠BCD=∠ACE}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△BDC≌△ACE(SAS),
∴BD=AE;
故答案为:BD=AE.
【类比探究】解:(2)BD=$\sqrt{2}$AE;理由如下:
如图2,过点D作DF∥AC,交BC于F.
∵DF∥AC,
∴∠ABC=∠DFB.
∵∠ABC=∠ACB=α,α=45°,
∴∠ABC=∠ACB=∠DFB=45°.
∴△DFB是等腰直角三角形
∴BD=DF=$\frac{\sqrt{2}}{2}$BF.
∵AE∥BC,
∴∠ABC+∠BAE=180°.
∵∠DFB+∠DFC=180°
∴∠BAE=∠DFC.
∵∠ABC+∠BCD=∠ADC,∠ABC=∠CDE=α,
∴∠ADE=∠BCD.
∴△ADE∽△FCD.
∴$\frac{AE}{DF}=\frac{AD}{CF}$.
∵DF∥AC,
∴$\frac{BD}{BF}=\frac{AD}{CF}$.
∴$\frac{AE}{BD}=\frac{BD}{BF}$=$\frac{\sqrt{2}}{2}$.
∴BD=$\sqrt{2}$AE,
故答案为:BD=$\sqrt{2}$AE.
(3)补全图形如图3,∵AE∥BC,∠EAC=∠ACB=α,
∴∠EAC=∠EDC=α,
∴A、D、C、E四点共圆,
∴∠ADE=∠ACE,
∵∠ADE+∠EDC=∠ADC=∠ABC+∠BCD,∠ABC=∠EDC=α,
∴∠ADE=∠BCD,
∴∠ACE=∠BCD
∵∠ABC=∠EAC=α,
∴△BDC∽△ACE,
∴$\frac{BD}{AE}=\frac{BC}{AC}$,
又∵$\frac{BC}{AC}$=2cosα,∴BD=2cosα•AE.
故答案为:BD=2cosα•AE.
点评 本题是三角形综合题目,考查了等边三角形的性质与判定、全等三角形的判定与性质以及三角形相似的判定与性质的综合应用,在解答本题时要注意类比思想的应用,正确绘图也是解题的关键.

 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )| A. | 14 cm | B. | 18 cm | C. | 24 cm | D. | 28 cm |
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
| 成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次考试成绩的众数是28分 | |
| C. | 该班学生这次考试成绩的中位数是28分 | |
| D. | 该班学生这次考试成绩的平均数是28分 |
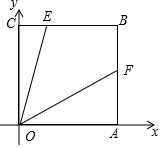 如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
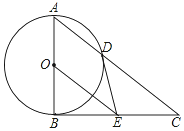 如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.