题目内容
17.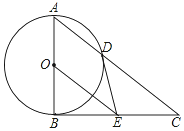 如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD•2OE;
(3)若cos∠BAD=$\frac{3}{5}$,BE=6,求OE的长.
分析 (1)利用圆周角定理得到∠ADB=90°,再利用直角三角形斜边上的中线性质得CE=DE=BE=$\frac{1}{2}$BC,则∠C=∠CDE,加上∠A=∠ADO得到∠C+∠A=90°,然后证明∠ODE=90°,从而根据切线的判定方法可判定DE为⊙O的切线;
(2)先证明OE是△ABC的中位线得到AC=2OE,再证明△ABC∽△BDC,则利用相似比和比例的性质可得到结论;
(3)利用OE∥AC得到∠BOE=∠BAD,根据余弦定义得到cos∠BOE=$\frac{3}{5}$=$\frac{OB}{OE}$,则可设OB=3t,OE=5t,利用勾股定理得到BE=4t,于是得到4t=6,然后求出t后计算5t即可.
解答 (1)解:连接BD、OD,如图,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E∵为斜边BC的中点,
∴CE=DE=BE=$\frac{1}{2}$BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)证明:∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴BC:CD=AC:BC,
即BC2=AC•CD.
∴BC2=2CD•OE;
(3)解:∵OE∥AC,
∴∠BOE=∠BAD,
在Rt△OBE中,cos∠BOE=$\frac{3}{5}$=$\frac{OB}{OE}$,
设OB=3t,OE=5t,
则BE=4t,
∴4t=6,解得t=$\frac{3}{2}$,
∴OE=5t=$\frac{15}{2}$.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、三角形中位线性质和切线的判定方法;会利用勾股定理和相似比计算线段的长和表示线段之间的关系.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案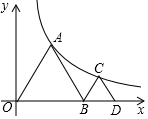 如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$+$\sqrt{6}$ | C. | 3$\sqrt{3}$+2$\sqrt{6}$ | D. | 2$\sqrt{6}$ |
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | c>a>b |
| A. | $\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | 3 | D. | -3 |
 如图,一大桥的桥拱为抛物线形,跨度AB=50米,拱高(即顶点C到AB的距离)为20米,求桥拱所在抛物线的表达式.
如图,一大桥的桥拱为抛物线形,跨度AB=50米,拱高(即顶点C到AB的距离)为20米,求桥拱所在抛物线的表达式. 如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.
如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.