题目内容
19.先化简($\frac{2}{a+1}$-$\frac{2a-3}{{a}^{2}-1}$)÷$\frac{1}{a+1}$,然后再从-2<a≤2的范围内选取一个合适的a的整数值代入求值.分析 先算括号里面的,再算除法,最后根据a的取值范围选出合适的a的值代入进行计算即可.
解答 解:原式=[$\frac{2(a-1)}{(a+1)(a-1)}$-$\frac{2a-3}{(a+1)(a-1)}$]•(a+1)
=$\frac{2(a-1)-(2a-3)}{(a+1)(a-1)}$•(a+1)
=$\frac{1}{(a+1)(a-1)}$•(a+1)
=$\frac{1}{a-1}$.
∵a+1≠0且a-1≠0,
∴a≠-1且a≠1.
又∵-2<a≤2且a为整数,
∴a=0或a=2.
当a=2时,原式=$\frac{1}{a-1}$=$\frac{1}{2-1}$=1.
点评 本题考查的是分式的化简求值,在解答此类问题时要注意a的取值保证分式有意义.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
4.若点A(a-2,a)在x轴上,则点B(a-1,3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知点A(-3,a)、B(-1,b)、C(2,c)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,则且a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | c>a>b |
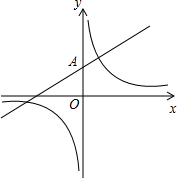 已知直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{m}{x}$的一个交点为(2,5),直线与y轴交于点A.
已知直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{m}{x}$的一个交点为(2,5),直线与y轴交于点A.