题目内容

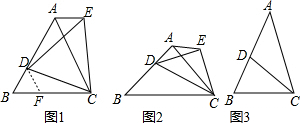
18．如图，在△ABC中，BD、CE是△ABC的中线，BD与CE相交于点0，点F、G分别是BO、CO的中点，连接AO．若AO=6cm，BC=8cm，则四边形DEFG的周长是（　　）
A．14 cmB．18 cmC．24 cmD．28 cm

分析 由中位线定理，可得EF∥AO，FG∥BC，且都等于边长BC的一半，据此可得出结论．

解答 解：∵BD，CE是△ABC的中线，
∴ED∥BC且ED=$\frac{1}{2}$BC，
∵F是BO的中点，G是CO的中点，
∴FG∥BC且FG=$\frac{1}{2}$BC，
∴ED=FG=$\frac{1}{2}$BC=4cm，
同理GD=EF=$\frac{1}{2}$AO=3cm，
∴四边形DEFG的周长=3+4+3+4=14（cm）．
故选A．

点评 本题考查了平行四边形的判定和三角形的中位线定理，三角形的中位线的性质定理，为证明线段相等和平行提供了依据．

练习册系列答案
相关题目
8．甲，乙，丙，丁四名跳高运动员赛前几次选拔赛成绩如表所示，根据表中的信息，如果要从中，选择一名成绩好又发挥稳定的运动员参加比赛，那么应选甲．
甲乙丙丁
平均数（cm）185180185180
方差3.63.67.98.2
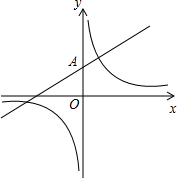9．已知直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{m}{x}$的一个交点为（2，5），直线与y轴交于点A．
（1）求m的值及点A的坐标；
（2）若点P在双曲线y=$\frac{m}{x}$的图象上，且S△POA=10，求点P的坐标．
6．计算
（1）（ab2•（-2a3b）3
（2）（-3a2b）（3a2-2ab+4b2）
（3）（6x4-4x3+2x2）÷（-2x2）
（4）（（x-5））（2x+5）-2x（x-3）
13．（1）先阅读，再填空：
（x+5）（x+6）=x2+11x+30；
（x-5）（x-6）=x2-11x+30；
（x-5）（x+6）=x2+x-30；
（x+5）（x-6）=x2-x-30．
观察上面的算式，根据规律，直接写出下列各式的结果：
（a+90）（a-100）=a2-10a-9000；        （y-80）（y-90）=y2-170y+7200．
（2）先阅读，再填空：（x-1）（x+1）=x2-1；（x-1）（x2+x+1）=x3-1；（x-1）（x3+x2+x+1）=x4-1；（x-1）（x4+x3+x2+x+1）=x5-1．
观察上面各式：①由此归纳出一般性规律：（x-1）（xn-1+xn-2+xn-3+…+x2+x+1）=xn-1；
②根据①直接写出1+3+32+…+367+368的结果$\frac{{3}^{69}-1}{2}$．
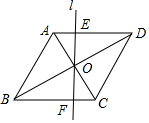3．如图，在菱形ABCD中，AB=2，∠ABC=60°，点O为对称中心，过点O的直线l交AD于点E，交BC于点F．
（1）求证：△AOE≌△COF；
（2）当∠AOE=30°时，求线段EF的长度．
10．计算：$\sqrt{25}$-$\root{3}{-27}$+$\sqrt{（-\frac{1}{2}）^{2}}$．
7．【问题情境】
数学课上，李老师提出了如下问题：在△ABC中，∠ABC=∠ACB=α，点D是AB边上任意一点，将射线DC绕点D逆时针旋转α与过点A且平行于BC边的直线交于点E．请判断线段BD与AE之间的数量关系．
小颖在小组合作交流中，发表自己的意见：“我们不妨从特殊情况下获得解决问题的思路，然后类比到一般情况．”小颖的想法获得了其他成员一致的赞成．
【问题解决】
如图1，当α=60°时，判断BD与AE之间的数量关系．
解法如下：过D点作AC的平行线交BC于F，构造全等三角形，通过推理使问题得到解决，请你直接写出线段BD与AE之间的数量关系：BD=AE．
【类比探究】
（2）如图2，当α=45°时，请判断线段BD与AE之间的数量关系，并进行证明；
（3）如图3，当α为任意锐角时，请直接写出线段BD与AE之间的数量关系：BD=2cosα•AE．（用含α的式子表示，其中0°＜α＜90°）
8．计算：
（1）$\sqrt{2\frac{1}{4}}$-$\root{3}{27}$+（π-3）0+|1-$\sqrt{3}$|；
（2）（-4x2y）2•（-xy2）÷（-2x5y3）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网