题目内容
4.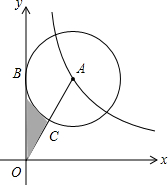 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )| A. | 4$\sqrt{3}$-$\frac{π}{3}$ | B. | 4$\sqrt{3}-\frac{2π}{3}$ | C. | 2$\sqrt{3}-\frac{π}{3}$ | D. | 2$\sqrt{3}-\frac{2π}{3}$ |
分析 连接AB,根据反比例函数系数k的几何意义得出S△AOB=2$\sqrt{3}$,根据点C为OA中点,得出AB=$\frac{1}{2}$OA,即可求得∠OAB=60°,根据面积求得AB的长,然后求得扇形的面积,即可求得阴影的面积.
解答  解:连接AB,BC,
解:连接AB,BC,
∵点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,
∴S△AOB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,
∴$\frac{1}{2}$OB•AB=2$\sqrt{3}$,
∵点C为OA中点,
∴BC=$\frac{1}{2}$OA=AC,
∴△ABC是等边三角形,
∴∠OAB=60°,
∴$\frac{OB}{AB}$=tan60°=$\sqrt{3}$,
∴OB=$\sqrt{3}$AB,
∴$\frac{1}{2}$•$\sqrt{3}$AB•AB=2$\sqrt{3}$,
∴AB=2,
∴S扇形=$\frac{60π•A{B}^{2}}{360}$=$\frac{60π•{2}^{2}}{360}$=$\frac{2π}{3}$,
∴S阴影=S△AOB-S扇形=2$\sqrt{3}$-$\frac{2π}{3}$,
故选D.
点评 本题考查了反比例函数系数k的几何意义,直角三角形斜边中线的性质,等边三角形的判定和性质以及扇形的面积等,作出辅助线构建等边三角形是解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
19.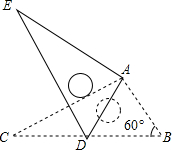 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
16.一个均匀的小立方体,它的6个面上分别标有实数5.1,$\frac{3}{4}$,$\sqrt{16}$,$\frac{π}{2}$,$\sqrt{11}$,8.$\stackrel{•}{2}0\stackrel{•}{3}$,任意掷出这个小立方体,朝上的面标有无理数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求:
如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求: 如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(-1,2),B(-4,1),C(-2,-2).
如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(-1,2),B(-4,1),C(-2,-2).